The Help Tutor Roll Aleven McLaren
Contents
- 1 Towards Tutoring Metacognition - The Case of Help Seeking
- 1.1 Meta-data
- 1.2 Abstract
- 1.3 Background and Significance
- 1.4 Glossary
- 1.5 Research questions
- 1.6 Independent Variables
- 1.7 Dependent variables
- 1.8 Hypothesis
- 1.9 Findings
- 1.9.1 Evaluation of goal 1: Capture metacognitive errors
- 1.9.2 Evaluation of goal 2: Improve metacognitive behavior
- 1.9.3 Evaluation of goal 3: Improve domain learning
- 1.9.4 Evaluation of goal 4: Improve future metacognitive behavior
- 1.9.5 Evaluation of goal 5: Improve future domain learning
- 1.9.6 Summary of results
- 1.10 Explanation
- 1.11 Connections
- 1.12 Further Information
- 1.13 Annotated bibliography
Towards Tutoring Metacognition - The Case of Help Seeking
Ido Roll, Vincent Aleven, Bruce M. McLaren, Kenneth Koedinger
Meta-data
PI's: Vincent Aleven, Ido Roll, Bruce M. McLaren, Ken Koedinger
Other Contributers: EJ Ryu (programmer)
| Study # | Start Date | End Date | LearnLab Site | # of Students | Total Participant Hours | DataShop? |
|---|---|---|---|---|---|---|
| 1 | 2004 | 2004 | Analysis of existing data | 40 | 280 | No, old data |
| 2 | 2005 | 2005 | Analysis of existing data | 70 | 105 | No, old data |
| 3 | 5/2005 | 5/2005 | Hampton & Wilkinsburg (Geometry) | 60 | 270 | No, incompatible format |
| 4 | 2/2006 | 4/2006 | CWCTC (Geometry) | 84 | 1,008 | Yes |
Abstract
While working with a tutoring system, students are expected to regulate their own learning process. However, often, they demonstrate inadequate metacognitive process in doing so. For example, students often ask for help too frequently or not frequently enough. In this project we built an Intelligent Tutoring System to teach metacognition, and in particular, to improve students' help-seeking behavior. Our Help Seeking Support Environment includes three components:
- Direct help seeking instruction, given by the teacher
- A Self-Assessment Tutor, to help students evaluate their own need for help
- The Help Tutor - a domain-independent agent that can be added as an adjunct to a cognitive tutor. Rather than making help-seeking decisions for the students, the Help Tutor teaches better help-seeking skills by tracing students actions on a (meta)cognitive help-seeking model and giving students appropriate feedback.
In a series of in vivo experiments, the Help Tutor accurately detected help-seeking errors that were associated with poorer learning and with poorer declarative and procedural knowledge components of help seeking. The main findings were that students made fewer help-seeking errors while working with the Help Tutor and acquired better help seeking declarative knowledge components. However, we did not find evidence that this led to an improvement in learning at the domain level or to better help-seeking behavior in a paper-and-pencil environment. We pose a number of hypotheses in an attempt to explain these results. We question the current focus of metacognitive tutoring, and suggest ways to reexamine the role of help facilities and of metacognitive tutoring within Intelligent Tutoring Systems.
Background and Significance
Not only that teaching metacognition holds the promise of improving current learning of the domain of interest, but also, or even mainly, it can accelerate future learning and successful regulation of independent learning. One example to metacognitive knowledge is help-seeking knowledge components: The ability to identify the need for help, and to elicit appropriate assistance from the [[relevant resources|help facilities]. However, considerable evidence shows that metacognitive knowledge components are in need of better support. For example, while working with Intelligent Tutoring Systems, students try to "game the system" or do not self-explain enough. Similarly, research shows that students' help-seeking behavior leaves much room for improvement.
Shallow help seeking knowledge components
Research shows that students do not use their help-seeking konwledge components approrpiately. For example, Aleven et al. (2006) show that 30% of students' actions were consecutive fast help requests (a common form of help abuse, termed 'clicking through hints'), without taking enough time to read the requested hints. Extensive log-file analysis suggests that students apply faulty knowledge components such as the following:
Faulty procedural knowledge components: Cognitive aspects:
If I don’t know the answer => I should guess
Motivational aspects:
If I get the answer correct => I achieved the goal
Social aspects:
If I ask for help => I am weak
Faulty declarative knowledge components:
Asking for hints will always reduce my skill level
Making an error is better than asking for a hint
Only weak people ask for help
Teaching vs. supporting metacognition
Several systems support students' metacognitive actions in a way that encourages, or even forces, students to learn productively and efficiently. For example, a tutoring system can require the student to self-explain. While this approach is likely to improve domain learning in the supported environment, the effect is not likely to persist beyond the scope of the tutoring system, and therefore is not likely to help students become better future learners.
Towards that end, we chose not to support students' help seeking actions, but to teach them better help-seeking skills. Rather than making the metacognitive decisions for the students (for example, by preventing help-seeking errors or gaming opportunities), this study focuses on helping students refine their Help Seeking knowledge components and acquire better feature validity of their help-seeking metacognitive skills.
By doing so, we examine whether metacognitive knowledge can be taught using familiar conventional domain-level pedagogies.
Glossary
Research questions
- Can conventional and well-established instructional principles in the domain level be used to tutor metacognitive knowledge components such as Help Seeking knowledge components?
- Does the practice of better metacognitive behavior translates, in turn, to better domain learning?
In addition, the project makes the following contributions:
- An improved understanding of the nature of help-seeking knowledge and its acquisition.
- A novel framework for the design of goals, interaction and assessment for metacognitive tutoring.
Independent Variables
Two studies were performed with the Help Tutor. In both studies the independent variable was the existence of help seeking support. Control condition used the conventional Geometry Cognitive Tutor
The treatment condition varied between studies:
- Study one: The Geometry Cognitive Tutor + the Help Tutor
- Study two: The Geometry Cognitive Tutor + the Help Seeking Support Environment (help seeking explicit instruction, self-assessment tutor, and Help Tutor)
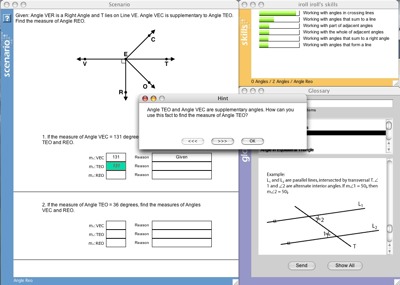
The Help Tutor:
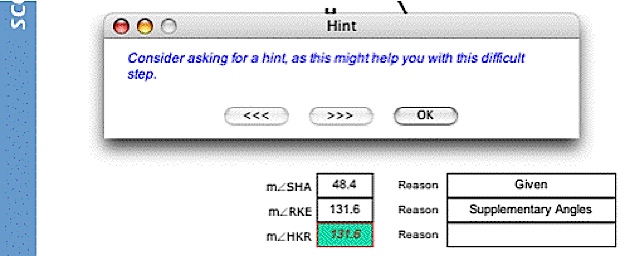
The Help Tutor is an a Cognitive Tutor in its own right that identifies recommended types of actions by tracing students’ interaction with the Geometry Cognitive Tutor relative to a metacognitive help-seeking model. When students perform actions that deviate from the recommended ones, the Help Tutor presents a message that stresses the recommended action to be taken. Messages from the metacognitive Help Tutor and the domain-level Cognitive Tutor are coordinated, so that the student receives only the most helpful message at each point [2].
The Self-Assessment Tutor: The ability to correctly self-assess one’s own knowledge level is correlated with strategic use of help (Tobias and Everson, 2002). The Self-Assessment Tutor is designed to tutor students on their self-assessment skills; to help students make appropriative learning decisions based on their self assessment; and mainly, to give students a tutoring environment, low on cognitive load, in which they can practice using their help-seeking skills. The curriculum used by the Treatment group in study two consists of interleaving Self Assessment and Cognitive Tutor + Help Tutor sessions, with the Self Assessment sessions taking about 10% of the students’ time. During each self-assessment session the student assesses the skills to be practiced in the subsequent Cognitive Tutor section.
Explicit help-seeking instruction: As White and Frederiksen demonstrated (1998), reflecting in the classroom environment on the desired metacognitive process helps students internalize it. With that goal in mind, we created a short classroom lesson about help seeking with the following objectives: to give students a better declarative understanding of desired and effective help-seeking behavior; to improve their dispositions and attitudes towards seeking help; and to frame the help-seeking knowledge as an important learning goal, alongside Geometry knowledge, for the coming few weeks. The instruction includes a video presentation with examples of productive and faulty help-seeking behavior and the appropriate help-seeking principles.
Dependent variables
The study uses two levels of dependent measures:
- Directly assessing Help Seeking skills
- Assessing domain-level learning, and by that evaluating the contribution of the help-seeking skills.
1. Assessments of help-seeking konwledge:
- Normal post-test:
- Declarative: hypothetical help-seeking dilemmas
- Procedural: Help seeking error rate while working with the tutor
- Transfer: Ability to use optional hints embedded within certain test items in the paper test.
2. Assessments of domain konwledge:
- Normal post-test: Problem solving and explanation items like those in the tutor's instruction.
- Transfer:
- Data insufficiency (or "not enough information") items.
- Conceptual understanding items (study two only)
Hypothesis
The combination of explicit help-seeking instruction, on-time feedback on help seeking errors, and raising awareness to knowledge deficits will
- Improve feature validity of students' help seeking skills
and thus, in turn, will
- Improve learning of domain knowledge by using those skills effectively.
Instructional Principles
The main principles being evaluated here is whether instruction should support meta-cognition in the context of problem solving by using principles of cognitive tutoring such as:
- Giving direct instruction
- Giving immediate feedback on errors
- Prompting for self-assessment
This utilizes the following instructional principles:
- The Self-Assessment Tutor utilizes the Reflection questions principle
- The Help Tutor itself utilizes the Tutoring feedback principle
- The Help Seeking Instruction utilizes the Explicit instruction principle.
Findings
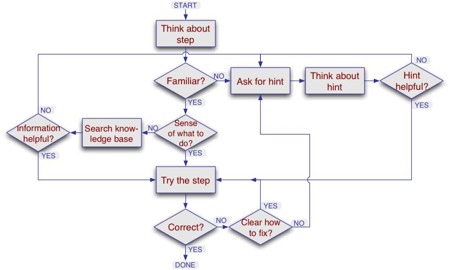
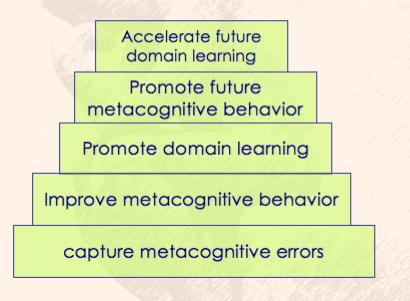
As seen below (adapted from Roll et al. 2006), metacognitive tutoring has the following goals:
- First, the tutoring system should capture metacognitive errors (in our case, help-seeking errors).
- Then, it should lead to an improved metacognitive behavior within the tutoring system.
- This, in turn, should lead to an improvement in the domain learning.
- The effect should persist beyond the scope of the tutoring system.
- As a result, students are expected to become better future learners.
Evaluation of goal 1: Capture metacognitive errors
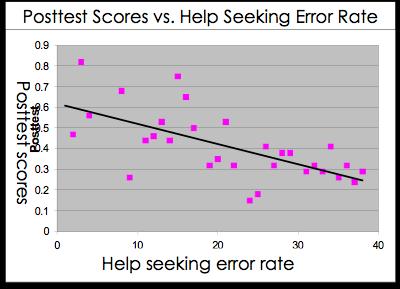
In study 1, 17% of students actions were classified as errors. These errors were singificantly negatively correlated with learning (r=-0.42) - the more help-seeking errors captured by the system, the smaller the improvement from pre- to post-test. This data suggests that the help-seeking model captures appropriate actions, and that the goal was achieved - the Help Tutor captures help-seeking errors.
Evaluation of goal 2: Improve metacognitive behavior
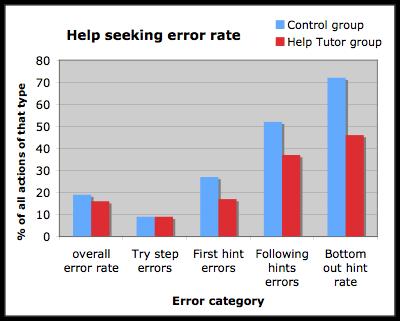
Log files from study 1 were analyzed to evaluate whether students improved their help-seeking behavior while working with the Help Tutor. While overall there was only a minor decrease in the error rate (from 19% in the control condition to 16% in the Help Tutor condition), there was a significant decrease in the error rate on first hints, following hints, and the portion of bottom-out hints out of all hint-sequences.
This data suggests that while the system was not able to improve all aspects of the desired metacognitive behavior, it did improve students' behavior on the common types of errors.
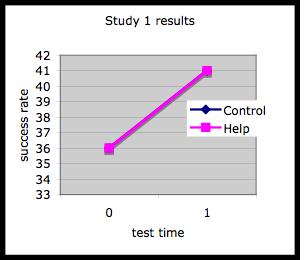
Evaluation of goal 3: Improve domain learning
While students' help seeking behavior improved while working with the Help Tutor (in study 1) or the full Help Seeking Support Environment (in study 2), we did not observe differences in learning between the two conditions on neither study 1 nor study 2.
Study 1 results:
Study 2 results:
- Notice, since the tests in times 1 and 2 evaluated different instructional units (Angles vs. Quadrilaterals), lower grades at time 2 do not suggest decrease in knowledge.
Evaluation of goal 4: Improve future metacognitive behavior
To evaluate whether the effect of the help-seeking curriculum persists beyond the tutored environment, students' help seeking behavior was evaluated in a transfer environment - the paper and pencil tests.
Hypothetical help seeking dilemmas, such as the one described below, were used to evaluate declarative help-seeking knowledge.
1. You tried to answer a question that you know, but for some reason the tutor says that your answer is wrong. What should you do? [ ] First I would review my calculations. Perhaps I can find the mistake myself? [ ] The Tutor must have made a mistake. I will retype the same answer again. [ ] I would ask for a hint, to understand my mistake.
Procedural help-seeking skills were evaluated using embedded hints in the tests (see figure in the Dependant Measures section above).
In study 1 (which included only the Help Tutor component,) students in the Treatment condition demonstrated neither better declarative nor procedural help-seeking knowledge, compared with the Control condition.
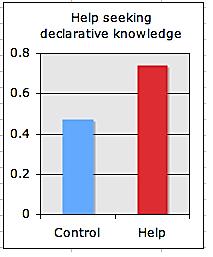
In study 2 (which included the explicit help-seeking instruction and the Self-Assessment tutor in addition to the Help Tutor) students in in the Treatment condition demonstrated better declarative help-seeking knowledge (compared with Control group students) but no better procedural knowledge
Evaluation of goal 5: Improve future domain learning
Due to technical difficulties, this goal was not evaluated in both studies.
Summary of results
Overall, the following pattern of results emerges from the studies: - The Help Seeking Support Environment intervened appropriate actions during the learning process - Students improved their help-seeking behavior while working with the system - Students acquired better help-seeking declarative knowledge following the system - However, students' domain learning did not improve - Also, the improvement in students' help seeking behavior did not persist beyond the tutoring system.
Explanation
These somewhat disappointing results raise an important question: Why did the environment not lead to an improvement in learning and in help-seeking behavior in the paper-test measures? Why did the improved online help-seeking behavior not lead to improved learning gains?
Hypothesis 1: Students do not have the skills, but we didn't teach them right.
One possible explanation may be that the Help Seeking Support Environment requires excessive cognitive load during problem solving. Clearly, the learning process with the Help Seeking Support Environment is more demanding compared with the conventional Cognitive Tutor alone, since more needs to be learned. However, much of the extra content is introduced during the classroom discussion and self-assessment sessions. The only extra content presented during the problem-solving sessions are the Help Tutor’s error messages, but they are not expected to increase the load much, especially given that a prioritization algorithm makes sure students receive only one message at a time (either from the Help Tutor or the cognitive tutor). Also, if the Help Seeking Support Environment indeed creates requires too much cognitive load, it should be expected to hinder learning, which we did not observe.
Hypothesis 2: The role of help seeking in ITS
Hints in tutoring systems have two objectives: to promote learning of challenging skills, and to help students move forward within the curriculum (i.e., to prevent them from getting stuck). While the latter is achieved easily with both the Cognitive Tutor and the Help Seeking Support Environment, achieving the first is much harder. It is not yet clear what makes a hint into a good hint, and how to create an effective hint sequence. It is possible that the hints, as implemented in the units of the Cognitive Tutor we used, are not optimal. For example, there may be too many levels of hints, with each level adding too little information to the previous one. Also, perhaps the detailed explanations are too demanding with regard to students’ reading comprehension ability. It is quite possible that these hints, regardless of how they are being used, are above students' zone of proximal development, and thus do not contribute much to learning. Support for that idea comes from Schworm and Renkl (2002). They found that offering explanations by the system impaired learning when self-explanation was required. The Geometry Cognitive Tutor prompts for self-explanation in certain units. Perhaps elaborated hints are redundant, or even damaging, when self-explanation is required. It is possible also that help-seeking behavior that we currently view as faulty may actually be useful and desirable, in specific contexts for specific students. For example, perhaps a student who does not know the material should be allowed to view the bottom-out hint immediately, in order to turn the problem into a solved example. Support for that idea can be found in a work by Yudelson et al. (2006), in which medical students in a leading med school successfully learned by repeatedly asking for more elaborated hints. Such “clicking-though hints” behavior would be considered faulty by Help Seeking Support Environment. However, this population of students is known to have good metacognitive skills (without them it is unlikely they would have reached their current position). Thus, it seems that sometimes “misusing” help (e.g., help abuse, according to the Help Seeking Support Environment) can be beneficial to some students. Further evidence can be found in Baker et al. (2004), who showed that some (but not all) students who “game the system” (i.e., click through hints or guess repeatedly) learn just as much as students who do not game. It may be the case that certain gaming behaviors are adaptive, and not irrational. Students who use these strategies will insist on viewing the bottom out hint and will ignore all intermediate hints, whether domain-level or metacognitive. Once intermediate hints are ignored, better help-seeking behavior according to the Help Seeking Support Environment should have no effect whatsoever on domain knowledge components, as indeed was seen. It is possible that we are overestimating students’ ability to learn from hints. Our first recommendation is to re-evaluate the role of hints in cognitive tutors using complementary methodologies such as log-file analysis (e.g., Chang (2006) uses dynamic Bayes nets to evaluate the contribution of hints in a reading tutor); tracing individual students (to evaluate the different uses students make of hints), experimentation of different types of hints (for example, proactive vs. on demand), and analysis of human tutors who aid students while working with cognitive tutors.
Hypothesis 3: The focus of metacognitive tutoring in ITS.
The previous hypothesis, focused on students’ tendency to skip hints, suggests that perhaps the main issue is not lack of knowledge, but lack of motivation. In other words, perhaps students already have these skills in place, but choose not to use them. For students who ignore intermediate hints, metacognitive messages offer little incentive. While the Help Seeking Support Environment can increase the probability that a proper hint level appears on the screen, it has no influence on whether it is being read, or whether the student attempts to understand it. Students may ignore the messages for several reasons. For example, they may habitually click through hints, and may resent the changes that the Help Seeking Support Environment imposes. This idea is consistent with the teachers’ observation that the students were not fond of the Help Seeking Support Environment error messages. They may comply with them, in order to make progress, but beyond that will ignore their content. The test data discussed above provides support for this idea. On 7 out of the 12 hint evaluations (seen in the findings section of goal 4) students scored lower on items with hints than on items with no hints. A cognitive headroom explanation does not account for this difference, since the Request hints did not add much load. A more likely explanation is that students chose to skip the hints since they were new to them in the given context. Baker (2005) reviewed several reasons for why students game the system. While no clear answer was given, the question is applicable here as well. Motivational issues bring us to our final hypothesis. Time preference discount (Feldstein, 1964) is a term coined in economics, that describes behavior in which people would rather have a smaller immediate reward over a distant greater reward. In the tutoring environment, comparing the benefit of immediate correct answer with the delayed benefit (if any) of acting metacognitively correct may often lead the student to choose the first. If that is indeed the case, then students may already have the right metacognitive skills in place. The question we should be asking ourselves is not only how to get students to learn the desired metacognitive skills – but mainly, how to get students to use them.
Connections
- The Help Tutor attempts to extend traditional tutoring beyond the common domains. In that, it is similar to the work of Amy Ogan on tutoring French Culture
- The manipulation of interaction between the student and the tutor, which is "natural" in the control condition, is guided by the help tutor. This is similar to the scripting manipulation of the Rummel Scripted Collaborative Problem Solving and the Walker A Peer Tutoring Addition projects.
- Another example for studying the effects of hints is Ringenberg's study, in which hints are compared to examples.
- Going to do an in-vivo study at a LearnLab site? Check out how to answer teacher's FAQ
Further Information
Plans for June 2007 - Dec. 2007:
- Present the study in the International Conference on Artificial Intelligence on Education
- Submit camera ready copy of the paper to the Journal on Metacognition and Instruction
- Analyze the logfiles for Metacognitive learning
Annotated bibliography
- Aleven, V., & Koedinger, K.R. (2000) Limitations of student control: Do students know when they need help? in proceedings of 5th International Conference on Intelligent Tutoring Systems, 292-303. Berlin: Springer Verlag. [pdf]
- Aleven, V., McLaren, B.M., Roll, I., & Koedinger, K.R. (2004) Toward tutoring help seeking - Applying cognitive modeling to meta-cognitive skills . in proceedings of 7th International Conference on Intelligent Tutoring Systems, 227-39. Berlin: Springer-Verlag. [pdf]
- Aleven, V., Roll, I., McLaren, B.M., Ryu, E.J., & Koedinger, K.R. (2005) An architecture to combine meta-cognitive and cognitive tutoring: Pilot testing the Help Tutor. in proceedings of 12th International Conference on Artificial Intelligence in Education, Amsterdam, The Netherlands: IOS press. [pdf]
- Aleven, V., McLaren, B.M., Roll, I., & Koedinger, K.R. (2006). Toward meta-cognitive tutoring: A model of help seeking with a Cognitive Tutor. Int Journal of Artificial Intelligence in Education(16), 101-30 [pdf]
- Baker, R.S., Corbett, A.T., & Koedinger, K.R. (2004) Detecting Student Misuse of Intelligent Tutoring Systems. in proceedings of 7Th International Conference on Intelligent Tutoring Systems, 531-40.
- Baker, R.S., Roll, I., Corbett, A.T., & Koedinger, K.R. (2005) Do Performance Goals Lead Students to Game the System? in proceedings of 12Th International Conference on Artificial Intelligence in Education, 57-64. Amsterdam, The Netherlands: IOS Press.
- Chang, K.K., Beck, J.E., Mostow, J., & Corbett, A. (2006) Does Help Help? A Bayes Net Approach to Modeling Tutor Interventions. in proceedings of Workshop on Educational Data Mining at AAAI 2006, 41-6. Menlo Park, California: AAAI.
- Feldstein, M.S. (1964). The Social Time Presence Discount Rate in Cost-Benefit Analysis. The Economic Journal 74(294), 360-79
- Roll, I., Baker, R.S., Aleven, V., McLaren, B.M., & Koedinger, K.R. (2005) Modeling Students’ Metacognitive Errors in Two Intelligent Tutoring Systems. in L. Ardissono, (Eds.), in proceedings of User Modeling 2005, 379-88. Berlin: Springer-Verlag. [pdf]
- Roll, I., Ryu, E., Sewall, J., Leber, B., McLaren, B.M., Aleven, V., & Koedinger, K.R. (2006) Towards Teaching Metacognition: Supporting Spontaneous Self-Assessment. in proceedings of 8th International Conference on Intelligent Tutoring Systems, 738-40. Berlin: Springer Verlag. [pdf]
- Roll, I., Aleven, V., McLaren, B.M., Ryu, E., Baker, R.S., & Koedinger, K.R. (2006) The Help Tutor: Does Metacognitive Feedback Improves Students' Help-Seeking Actions, Skills and Learning? in proceedings of 8th Int C on Intelligent Tutoring Systems, 360-9. Berlin: Springer Verlag. [pdf]
- Roll, I., Aleven, V., McLaren, B. M., & Koedinger, K. R. (2007). Can help seeking be tutored? Searching for the secret sauce of metacognitive tutoring. International Conference on Artificial Intelligence in Education, , 203-10. [pdf]
- Roll, I., Aleven, V., McLaren, B. M., & Koedinger, K. R. (2007). Designing for metacognition - applying cognitive tutor principles to the tutoring of help seeking. Metacognition and Learning, 2(2). [pdf]
- Schworm, S., & Renkl, A. (2002) Learning by solved example problems: Instructional explanations reduce self-explanation activity. in proceedings of The 24Th Annual Conference of the Cognitive Science Society, 816-21. Mahwah, NJ: Erlbaum.
- Yudelson, M.V., Medvedeva, O., Legowski, E., Castine, M., Jukic, D., & Crowley, R.S. (2006) Mining Student Learning Data to Develop High Level Pedagogic Strategy in a Medical ITS. in proceedings of Workshop on Educational Data Mining at AAAI 2006, Menlo Park, CA: AAAI.# Roll, I., Aleven, V., & Koedinger, K.R. (2004) Promoting Effective Help-Seeking Behavior through Declarative Instruction. in proceedings of 7th International Conference on Intelligent Tutoring Systems, 857-9. Berlin: Springer-Verlag. [pdf]