Ringenberg Examples-as-Help

Scaffolding Problem Solving with Embedded Examples to Promote Deep Learning

Michael Ringenberg and Kurt VanLehn

Summary Table

PIs	Kurt VanLehn, Donald Treacy, Michael Ringenberg
Study Start Date	18 February 2005
Study End Date	04 April 2005
LearnLab Site	USNA
LearnLab Course	General Physics II
Number of Students	N = 46
Total Participant Hours	20 minutes over required coursework
DataShop	No; Andes data still incompatible

Abstract

This in vivo experiment which occurred in the Physics LearnLab compared the relative utility of an intelligent tutoring system that used hint sequences to a version that used completely justified examples for learning college level physics. In order to test which strategy produced better gains in competence, two version of Andes were used: one offered participants hint sequences and the other completely justified examples in response to their help requests. We found that providing examples was at least as effective as the hint sequences and was more efficient in terms of the number of problems it took to obtain the same level of mastery.

Background and Significance

When students use a tutoring system with hint sequences, they sometimes engage in help abuse on virtually every step (citation needed). This means that the tutoring system is telling them each step, so essentially, they are generating a worked-out example. There may be nothing wrong with this for some students, as examples can be effective instructional material (citation needed).

Glossary

See Ringenberg Examples-as-Help Glossary

Research question

Will robust learning ensue if students are presented with relevant, completely justified examples instead of hint sequences whenever they ask for a help?

Independent variables

Particpants worked on assigned homework problems covering Inductors by using Andes at home. When they requested help on a step, they got either:

• a relevant, completely justified example (the Examples condition), or

• the normal Andes hint sequence (the Hints condition).

When they clicked on the "Done" button the example or the hint would disappear, then they would be back in problem solving mode. Thus, Examples students could not easily copy steps from the example to the problem they were solving.

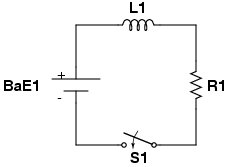
Figure 1: A screenshot of Andes Physics Workbench

Figure 2: A worked-out example. A window would pop-up containing a relevant example if a participant in the experimental condition asked for help while solving problems in Andes. This is the example that was paired with the problem in Figure 1. Each Source field in the equation table was either a list of the indexes to the equations combined or simplified to produce the given equation or the name of the principle used. The principle name were linked to a textbook page covering the topic and the pages were available to all participants. The italic text in the Source field was a tooltip that would appear if the participant moused over the source. Bold equations indicate sought quantities.

Problem Statement  In the circuit below, the current through the resistor rises from zero at 0.0 s to 40% of its maximum value at 4.0 s. The inductor has a self-inductance of 10H and the battery has a Vb of 12 V. What is the resistance of R1? What is the current through R1 at 4.0 s? Solution Variables T0 = switch is closed T1 = 4.0 s later T2 = "infinity" (a long time later) L1 = inductance of L1 R1 = Resistance of R1 Vb = Voltage across BaE1 at time T0 to T2 τ = time constant of circuit containing L1 t = duration of time from T0 to T1 I1 = Current through R1 at time T1 I2 = Current through R1 at time T2 Equations Equation Source 1. L1 = 10 H Given (This information is from the problem statement) 2. Vb = 12 V Given (This information is from the problem statement.) 3. t = 4 s Given (This information is from the problem statement.) 4. L1 = 10 H Given (This information is from the problem statement.) 5. I1 = 0.4 * I2 Given (This information is from the problem statement.) 6. I1 = I2 * (1-exp(-t/τ)) LR current growth (I=Ifull * (1-e(-t/τ))) 7. 0.4 * I2 = I2 * (1-exp(-t/τ)) 6,5 8. 0.4 = (1-exp(-4 s/τ)) 7,3 9. τ = 0.128 s 8 10. τ = L1/R1 LR Time constant (τ = L / R) 11. 0.128 s = 10 H/R1 10,9,1 12. R1 = 78.3 ohm 11 13. I2 = Vb/R1 LR current fully charged (Ohm's Law: I = Vb / R) 14. I2 = 12 V/78.3 ohm 13,2,11 15. I2 = 0.153 A 14 16. I1 = 0.4 * 0.153 A 5,14 17. I1 = 0.0612 A 16

Figure 3: A Hint sequence from Andes. This is a possible hint sequence which is displayed in the lower left hand window of the Andes Physics Workbench if a participant asked for help in the control condition. "T:" indicates messages from the tutoring system. "S:" indicates input from the student/participant via menus.

T: You should finish entering all of the useful given quantities in
   the problem.  Why don't you work on entering the given value of the
   inductance of L1.
        Explain further OK

T: You can find the value of the inductance of L1 in the problem
   statement.

T: The value of the inductance of L1 is given as 3.2 H.

T: Enter the equation L1 = 3.2 H.
        OK

Figure 4: Another Andes hint sequence. Again, this is a possible hint sequence available to participants in the control condition if they asked for help. "T:" indicates messages from the tutoring system. "S:" indicates input from the student/participant via menus.

T: Now that you have stated all of the given information, you should
   start on the major principles. What quantity is the problem seeking?
S: The Voltage across L1 at time T0 to T1.

T: That's right. What is the first principle application that you
   would like to work on? Hint: this principle application will
   usually be one that mentions the sought quantity
   explicity. Therefore it's equation may contain the sought quantity
   that the problem seeks.
S: V= -L*dI/dt   Inductor EMF

Hypothesis

Providing completely justified examples instead of hint sequences when students ask for help on steps will promote the learning of knowledge components and help appropriately generalize the knowledge components.

Dependent variables & Results

Near Transfer, retention

Performance on problems involving inductors on the normal mid-term exam that were similar to the training problems. There was not significant difference in performance between the two conditions. Both conditions did better than a baseline of participants who solved no homework problems.

Transfer task, deep structure assessment

Problem matching task: No significant difference in performance between the two conditions; however, participants in the examples condition solved fewer training problems. Both conditions did better than a baseline of participants who solved no homework problems.

Homework

Number of problems completed: Participants in the examples condition solved significantly fewer problems than participants in the hints condition.

Time on task: Participants in the examples condition spent less time solving problems than those in the hints condition. Participants in both conditions spent about the same amount of time per problem.

Annotated bibliography

• Ringenberg, Michael A. & VanLehn, Kurt (2006). Scaffolding Problem Solving with Annotated, Worked-Out Examples to Promote Deep Learning. Paper presented at the ITS 2006, Taiwan. Winner of Best Paper First Authored by a Student Award. 231Kb PDF