Difference between revisions of "Rummel Scripted Collaborative Problem Solving"
DejanaDiziol (talk | contribs) (→Background and Significance) |
(→Connections) |
||
| (120 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
== Collaborative Extensions to the Cognitive Tutor Algebra: Scripted Collaborative Problem Solving == | == Collaborative Extensions to the Cognitive Tutor Algebra: Scripted Collaborative Problem Solving == | ||
| − | ''Nikol Rummel, Dejana Diziol, Bruce McLaren, and Hans Spada'' | + | ''Nikol Rummel, Dejana Diziol, Bruce M. McLaren, and Hans Spada'' |
| + | |||
| + | === Summary Tables === | ||
| + | {| border="1" cellspacing="0" cellpadding="5" style="text-align: left;" | ||
| + | | '''PIs''' || Bruce McLaren, Nikol Rummel & Hans Spada | ||
| + | |- | ||
| + | | '''Other Contributers''' || | ||
| + | * Graduate Student: Dejana Diziol | ||
| + | * Staff: Jonathan Steinhart, Pascal Bercher | ||
| + | |} | ||
| + | <br> | ||
| + | '' Pre Study '' | ||
| + | {| border="1" cellspacing="0" cellpadding="5" style="text-align: left;" | ||
| + | | '''Study Start Date''' || 03/13/06 | ||
| + | |- | ||
| + | | '''Study End Date''' || 03/21/06 | ||
| + | |- | ||
| + | | '''LearnLab Site''' || CWCTC | ||
| + | |- | ||
| + | | '''LearnLab Course''' || Algebra | ||
| + | |- | ||
| + | | '''Number of Students''' || ''N'' = 30 | ||
| + | |- | ||
| + | | '''Average # of hours per participant''' || 3 hrs. | ||
| + | |- | ||
| + | | '''Data in DataShop''' || yes | ||
| + | |} | ||
| + | <br> | ||
| + | |||
| + | '' Full Study '' | ||
| + | {| border="1" cellspacing="0" cellpadding="5" style="text-align: left;" | ||
| + | | '''Study Start Date''' || 04/03/06 | ||
| + | |- | ||
| + | | '''Study End Date''' || 04/07/06 | ||
| + | |- | ||
| + | | '''LearnLab Site''' || CWCTC | ||
| + | |- | ||
| + | | '''LearnLab Course''' || Algebra | ||
| + | |- | ||
| + | | '''Number of Students''' || ''N'' = 139 | ||
| + | |- | ||
| + | | '''Average # of hours per participant''' || 3 hrs. | ||
| + | |- | ||
| + | | '''Data in DataShop''' || yes | ||
| + | |} | ||
| + | <br> | ||
=== Abstract === | === Abstract === | ||
| − | In this project, the Algebra I Cognitive Tutor is extended to a [[ | + | In this project, the Algebra I Cognitive Tutor is extended to a [[collaborative learning environment]]: students learn to solve system of equations problems while working in dyads. As research has shown, collaborative problem solving and learning has the potential to increase elaboration on the learning content. However, students are not always able to effectively meet the challenges of a collaborative setting. To ensure that students capitalize on collaborative problem solving with the Tutor, a [[collaboration scripts|collaboration script]] was developed that guides their interaction and prompts fruitful [[collaboration]]. During the scripted problem solving, students alternate between individual and collaborative phases. Furthermore, they reflect on the quality of their interaction during a recapitulation phase that follows each problem they solve. During this phase, students self evaluate their interaction and plan how to improve it, thus they engage in [[metacognition|metacognitive activities]]. |
| − | To assess the effectiveness of the script, we conducted two classroom studies. In an initial, small scale study (pre study) that served to establish basic effects and to test the procedure in a classroom setting, we compared scripted collaboration with an unscripted collaboration condition in which students collaborated without support. In the full study, we furthermore compared these collaborative conditions to an individual condition to assess the effect of the collaborative Tutor extension to regular Tutor use. The experimental learning phase took place on two days of instruction. On the third day, during the test phase, students | + | To assess the effectiveness of the script, we conducted two classroom studies. In an initial, small scale study (pre study) that served to establish basic effects and to test the procedure in a classroom setting, we compared scripted collaboration with an unscripted collaboration condition in which students collaborated without support. In the full study, we furthermore compared these collaborative conditions to an individual condition to assess the effect of the collaborative Tutor extension to regular Tutor use. The experimental learning phase took place on two days of instruction. On the third day, during the test phase, students completed several post tests that assessed [[robust learning]]. Results from the [[transfer]] test of the pre study revealed significant differences between conditions: Students that received script support during collaboration showed higher mathematical understanding and were better at reasoning about mathematical concepts. In the full study, results varied for the different measures of [[robust learning]]: While students of the scripted condition had a slight disadvantage when the script was removed for the first time (collaborative [[normal post-test|retention]]; note: only for students in the scripted condition, the problem-solving situation was different than during instruction), this disadvantage could no longer be found in the second retention test (individual [[normal post-test|retention]]). The [[transfer]] test revealed that students that learned collaboratively were better at reasoning about mathematical concepts. Finally, students of the scripted condition were better prepared for [[accelerated future learning|future learning]] situations than students that collaborated without script support. |
=== Background and Significance === | === Background and Significance === | ||
| − | In our project, we combined two different [[instructional method]]s both of which have been shown to improve students’ learning in mathematics: Learning with intelligent tutoring systems (Koedinger, Anderson, Hadley, & Mark, 1997) and collaborative problem solving (Berg, 1993). The Cognitive Tutor Algebra that was used in our study is a tutor for mathematics instruction at the high school level. | + | In our project, we combined two different [[instructional method]]s both of which have been shown to improve students’ learning in mathematics: Learning with intelligent tutoring systems (Koedinger, Anderson, Hadley, & Mark, 1997) and collaborative problem solving (Berg, 1993). The [[Cognitive tutor|Cognitive Tutor]] Algebra that was used in our study is a tutor for mathematics instruction at the high school level. Students learn with the Tutor during part of the regular classroom sessions. The Tutor's main features are immediate error feedback, the possibility to ask for a hint when encountering impasses, and knowledge tracing, i.e. the Tutor creates and updates a model of the student’s knowledge and selects new problems tailored to the student’s knowledge level. Although several studies have proven its effectiveness, students do not always benefit from learning with the Tutor. First, because the Tutor places emphasis on learning [[procedural|procedural problem solving skills]], yet a deep understanding of underlying mathematical [[conceptual knowledge|concepts]] is not necessarily achieved (Anderson, Corbett, Koedinger, & Pelletier, 1995). Second, students do not always make good use of the learning opportunities provided by the Cognitive Tutor (e.g. [[help abuse]], see Aleven, McLaren, Roll, & Koedinger, 2004; [[game the system|gaming the system]], Baker, Corbett, & Koedinger, 2004). So far, the Cognitive Tutor has been used in an individual learning setting only. However, as research on collaborative learning has shown, collaboration can yield elaboration of learning content (Teasley, 1995), thus this could be a promising approach to reduce the Tutor’s shortcomings. On the other hand, students are not always able to effectively meet the challenges of a collaborative setting (Rummel & Spada, 2005). [[Collaboration scripts]] have proven effective in helping people meet the challenges encountered when learning or working collaboratively (Kollar, Fischer, & Hesse, in press). To ensure that students would profit from a collaboratively enhanced Tutor environment, we thus developed a collaboration script that prompts fruitful interaction on the Tutor while students learned to solve “systems of equations”, a content novel to the participating students. The script served two goals: First, to improve students’ [[robust learning]] of [[knowledge component|knowledge components]] relevant for the systems of equation units (i.e. both problem solving skills and understanding of the concepts). Second, students should increase their explicit knowledge of what constitutes a fruitful collaboration and improve their [[collaboration skill]]s in subsequent interactions without further script support. This is particularly important due to the risk of overscripting collaboration that has been discussed in conjunction with scripting for longer periods of time (Rummel & Spada, 2005). |
=== Glossary === | === Glossary === | ||
See [[:Category:Scripted Collaborative Problem Solving|Scripted Collaborative Problem Solving Glossary]] | See [[:Category:Scripted Collaborative Problem Solving|Scripted Collaborative Problem Solving Glossary]] | ||
| − | + | === Research question === | |
| + | Does [[collaboration]] – and in particular [[collaboration scripts|scripted collaboration]] – improve students’ [[robust learning]] in the domain of algebra? | ||
| − | + | Does the [[collaboration scripts|script]] approach improve students’ collaboration, and does this result in more [[robust learning]] of the algebra content? | |
| − | + | === Independent variables === | |
| + | The independent variable was the [[instructional method|mode of instruction]]. Three conditions were implemented in the learning phase that took place on two days of instruction: | ||
| − | *[[Collaborative Problem-Solving | + | * ''Individual condition'': Students solved problems with the Algebra I Cognitive Tutor in the regular fashion (i.e. computer program as additional [[agent]]). |
| − | + | * ''Unscripted collaborative condition'': Students solved problems on the Cognitive Tutor while working in dyads; thus, a second learning resource was added to the regular Tutor environment (i.e., both a peer and a computer program as additional [[agent]]s). | |
| − | *[[ | + | * ''Scripted collaboration condition'': As in the unscripted collaborative condition, students solved problems on the Tutor while working in dyads; however, their dyadic problem solving was guided by the ''Collaborative Problem-Solving Script (CPS)'' (i.e., both a peer and a computer program as additional [[agent]]s; for an overview of the script structure, see Figure 1). Three script components supported their interaction in order to reach a more fruitful collaboration and improved learning: |
| − | + | **A fixed script component structured students’ collaboration in an individual and a collaborative phase (see Figure 1). During the individual phase, each student solved a single equation problem; during the collaborative phase, these problems were combined to a more complex system of equations problem. This division of expertise aimed at increasing the individual's responsibility for the common problem-solving process and thus at yielding a more fruitful interaction. In addition, the fixed script component structured the collaborative phase in several sub steps and prompted students to engage in [[elaborative interaction]] (see Figure 2 and 3). | |
| − | *[[ | + | **An adaptive script component provided prompts to improve the collaborative learning process when the dyad encountered difficulties in their problem solving. E.g., to prevent [[help abuse]] in the tutoring system and to stop students from proceeding in the [[hint sequence]] until reaching the [[bottom out hint]], the dyad is prompted to [[elaborative interaction|elaborate]] on the Tutor hints when reaching the penultimate hint of the hint sequence (see Figure 4). This aims at enabling students to find the answer by themselves on basis of the help received and at students gaining knowledge to solve similar steps later on their own. |
| + | **A [[metacognition|metacognitive]] script component prompted students to engage in reflection of the group process to improve their collaboration over subsequent interactions. Following each collaborative phase, students rated their interaction on 8 [[collaboration skill]]s and set goals for the following collaboration. This phase was referred to as the "recapitulation phase" | ||
| − | + | <br> | |
| + | Figure 1. Structure of the Collaborative Problem-Solving Script.<br> | ||
| + | [[Image:CPS design.jpg]] | ||
| − | + | Figure 2 and 3. Screenshot of the enhanced Cognitive Tutor Algebra: Instructions for the following sub step (for details, see figure 3; responsibilities for student A and B marked by color of text.<br> | |
| + | [[Image:Enhanced CTA environment.jpg]] | ||
| − | + | [[Image:Instruction detailed.jpg]] | |
| − | + | <br>Figure 4. Adaptive script prompt: penultimate hint message (appeared when students clicked on "next hint" to reach the bottom-out hint).<br><br> | |
| − | + | [[Image:Penultimate hint.jpg]] | |
| − | + | <br>In all conditions, the Cognitive Tutor supported students’ problem solving by flagging their errors and by providing on-demand hints. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | In all conditions, the Cognitive Tutor supported students’ problem solving by flagging their errors and by providing on-demand hints. | ||
Communication between the collaborative partners in the collaborative conditions was face to face: they joined together at a single computer to solve the problems. In the scripted collaboration condition, the script structured the allocation of subtasks between the two students. | Communication between the collaborative partners in the collaborative conditions was face to face: they joined together at a single computer to solve the problems. In the scripted collaboration condition, the script structured the allocation of subtasks between the two students. | ||
| Line 53: | Line 92: | ||
=== Hypothesis === | === Hypothesis === | ||
| − | The hypothesis can be stated in two parts: knowledge gains in the domain of algebra and improvement of the dyads’ collaboration | + | The hypothesis can be stated in two parts: knowledge gains in the domain of algebra and improvement of the dyads’ [[collaboration skill]]s: |
| − | # We expect the collaborative conditions – in particular the scripted collaboration condition – to outperform the individual conditions in measures of robust learning of the algebra content. | + | # We expect the [[collaboration|collaborative conditions]] – in particular the [[Collaboration scripts|scripted collaboration]] condition – to outperform the individual conditions in measures of robust learning of the algebra content. |
| − | # We expect that problem-solving with the Collaborative Problem-Solving Script will lead to a more effective interaction than unscripted collaboration in the learning phase. In addition, we expect that the newly gained | + | # We expect that problem-solving with the [[Collaboration scripts|Collaborative Problem-Solving Script]] will lead to a more effective interaction than unscripted collaboration in the learning phase. In addition, we expect that the newly gained [[collaboration skill]]s will sustain during subsequent collaborations in the test phase when script support is no longer available. |
=== Dependent variables === | === Dependent variables === | ||
| − | Students | + | Students took several post tests during the test phase that took place two days after instruction: |
| − | * '' | + | * ''[[Normal post-test]] (retention)'': Two post-tests measured immediate retention. As during the learning phase, students solved system of equations problems on the Cognitive Tutor. The problems were “isomorphic” to those in the instruction, but had different content. One test was solved collaboratively to measure both students’ algebra skills and their collaboration skills, the other test was solved individually to assess if the students were able to generalize the gained knowledge to isomorphic problems when working on their own. |
| − | + | * ''[[Transfer]]'': This paper and pencil test assessed students' understanding of the main mathematical concepts from the learning phase: slope, y-intercept and intersection point. The [[conceptual tasks]] students had to solve tapped the same [[knowledge components]] as the problems in instruction; however, the problems where non-isomorphic to those in the instruction, thus demanded students to flexibly apply their knowledge to problems with a new format. The test consisted of two problem sets with two different question formats: problem set 1 asked for the basic concepts y-intercept and slope, problem set 2 asked for the novel system’s concept of intersection point. Both sets were composed of questions with a distinct answer format and open format questions that asked students to explain their problem-solving. | |
| − | * '' | + | * ''[[Accelerated future learning]]'': To measure accelerated future learning, students learned how to solve problems in a new area of algebra – inequality problems. This test was administered on the Cognitive Tutor, thus students could ask the Tutor for hints and received immediate error feedback. According to their condition during the experimental learning phase, they either worked individually or collaboratively on this post test. However, in contrast to the learning phase, they did not receive additional instructions to support their collaboration. |
| − | * ''[[Accelerated future learning]]'': To measure accelerated future learning, students learned how to solve problems in a new area of algebra – inequality problems | ||
| − | Several variables from these post tests are compared to test the two | + | Several variables from these post tests are compared to test the two hypotheses. |
| − | + | * For the post tests conducted on the Cognitive Tutor (retention and accelerated future learning), we extracted 3 variables from the Tutor logfiles. | |
| − | + | ** ''[[error rate]]'' | |
| + | ** ''[[assistance score]]'' | ||
| + | ** the process variable ''elaboration time'' measures the average time spent after errors, bugs and hints. These are regarded as potential [[learning events]]: if students spend more time elaborating on their impasses, they can increase their knowledge and thus improve their problem-solving in subsequent problems. This variable was used as an indicator for [[sense making|deep learning processes]] during problem solving. | ||
| + | *For the paper and pencil post test (far transfer), we developed a scoring systems. For distinct format questions, students received 0 points for incorrect/missing answers and 1 point for correct answers; for open format questions , students received 0 points for incorrect, irrelevant or missing answers, 1 point for partly elaborated answers, and 2 points for fully elaborated answers. We summed points separately for the two question formats and the two problem sets of this post-test, resulting in four variables. | ||
| + | *To compare [[collaboration skill]]s of students, we recorded students’ dialogues both during learning phase and during test phase. Based on the analysis method reported in Meier, Spada, and Rummel (2007), we developed a rating scheme that assesses students’ interaction from two different perspectives. With the first perspective, we evaluate the quality of their collaborative problem-solving, e.g. if they capitalize on the social resource and on the system resource to improve their learning. From the second perspective, we evaluate the quality of their interaction with dimensions such as “mathematical elaboration” and “dyad’s motivation”. We applied the rating scheme to our process data using ActivityLens (Avouris, Fiotakis, Kahrimanis, Margaritas, & Komis, 2007), a software tool that permits the integration of several data sources, in this case the integration of CTA log data and the audio and screen recordings from students' collaboration at the CTA. <br>These process analyses are part of an international collaboration with the research group of Nikos Avouris, University of Patras, Greece, in the context of the Kaleidoscope Network of Excellence project [http://cavicola.noe-kaleidoscope.org/ CAViCoLA] (Computer-based Analysis and Visualization of Collaborative Learning Activites). Further information on these analyses can be found in Diziol et al. (paper accepted for presentation at the ICSL 2008, Utrecht). | ||
=== Method === | === Method === | ||
| − | The study procedure took place during 3 classroom periods over the course of a week. During day 1 and day 2 (the learning phase), the experimental conditions (i.e. the independent variables) were implemented. On day 3, students had to solve several post-tests that assessed different aspects of robust learning. | + | The study procedure took place during 3 classroom periods over the course of a week. During day 1 and day 2 (the learning phase), the experimental conditions (i.e. the independent variables) were implemented. On day 3, students had to solve several post-tests that assessed different aspects of [[robust learning]]. |
| − | Two in vivo classroom studies were conducted: a pre study with 3 classrooms, and a full study with 8 classrooms. The pre study aimed at establishing basic effects of the script and testing the procedure in a classroom setting, thus we only compared scripted to unscripted collaboration. In the full study, we compared the scripted collaboration condition to both an individual condition and an unscripted collaboration to evaluate the merits of both enhancing the Tutor with collaboration in general and scripted collaboration in particular. Due to the disruptiveness of students in the same class using different interventions, we used a between-class design. | + | Two in vivo classroom studies were conducted: a pre study with 3 classrooms, and a full study with 8 classrooms. The pre study aimed at establishing basic effects of the [[collaboration scripts|script]] and testing the procedure in a classroom setting, thus we only compared scripted to unscripted collaboration. In the full study, we compared the scripted collaboration condition to both an individual condition and an unscripted collaboration to evaluate the merits of both enhancing the Tutor with collaboration in general and scripted collaboration in particular. Due to the disruptiveness of students in the same class using different interventions, we used a [[between classroom design|between-class design]]. |
'''Participants pre study:''' | '''Participants pre study:''' | ||
| Line 81: | Line 123: | ||
'''Participants full study:''' | '''Participants full study:''' | ||
* Individual condition: 1 class (21 students) | * Individual condition: 1 class (21 students) | ||
| − | * Unscripted condition: 3 classes ( | + | * Unscripted condition: 3 classes (18 + 16 + 16 dyads = 25 dyads) |
| − | * Scripted condition: 4 classes ( | + | * Scripted condition: 4 classes (16 + 16 + 18 + 18 dyads = 34 dyads) |
=== Findings === | === Findings === | ||
| + | |||
| + | The study was conducted at a vocational high school: Half a day, students took vocational classes (e.g. carpentry, cooking) and mathematics at the vocational school, half a day, they took the regular lessons at their home schools. This yielded a high rate of students’ absenteeism, and as a consequence, we had to exclude some dyads from further data analysis. We restricted the analysis to students that met the following criteria: they were present at least during one day of instruction, they were present at the test day, and they always worked according to their condition when present. For instance, a student from one of the collaborative conditions that worked individually on one day was excluded from further data analysis. The resulting participant numbers for data analysis in the two studies are reported in the respective findings sections. | ||
| + | |||
'''Findings pre study:''' | '''Findings pre study:''' | ||
| − | + | In the pre study, nine students from the unscripted and ten students from the scripted condition met the criteria to be included in the data analysis. Since the subject number in the collaborative post tests is rather small, we’ll concentrate on the results of the paper and pencil post test (far transfer) that was solved individually. This test revealed substantial differences between conditions. | |
| − | Significant differences were found both in the MANOVA (Pillai-Spur, F(4, 14) = 7.35, p < .05) and in subsequent ANOVAs. Multiple choice answers on basic concepts did not show a significant difference, F(1,17) = 2.26, ns. However, the scripted condition outperformed the unscripted condition on the discrete answer questions about the system’s concept, F(1,17) = 22.16, p < .01. A significant difference between conditions was also found for the open format questions of both problem sets with F(1,17) = 5.85, p < .05 for the basic concepts and F(1,17) = 17.01, p < .01 for the system’s concept. Particularly the results of the open format questions demonstrate the script’s effect on conceptual knowledge acquisition: after scripted interaction during the learning phase, students were better at articulating their mathematical thinking compared to their unscripted counterparts. However, it should be noted that in general students in both conditions had difficulties providing explanations, thus only reached low scores in the open format questions. The amount of wrong explanations and the number of students who did not even try to articulate their thinking was very high. | + | Significant differences were found both in the MANOVA (Pillai-Spur, F(4, 14) = 7.35, p < .05) and in subsequent ANOVAs. Multiple choice answers on basic concepts did not show a significant difference, F(1,17) = 2.26, ns. However, the scripted condition outperformed the unscripted condition on the discrete answer questions about the system’s concept, F(1,17) = 22.16, p < .01. A significant difference between conditions was also found for the open format questions of both problem sets with F(1,17) = 5.85, p < .05 for the basic concepts and F(1,17) = 17.01, p < .01 for the system’s concept. |
| + | Particularly the results of the open format questions demonstrate the script’s effect on [[conceptual knowledge]] acquisition: after scripted interaction during the learning phase, students were better at articulating their mathematical thinking compared to their unscripted counterparts. However, it should be noted that in general students in both conditions had difficulties providing explanations, thus only reached low scores in the open format questions. The amount of wrong explanations and the number of students who did not even try to articulate their thinking was very high. | ||
| − | + | '''Findings full study:''' | |
| + | |||
| + | In the full study, 17 students from the individual condition, 19 dyads (40 students) from the unscripted condition and 23 dyads (49 students) from the scripted condition were included in data analysis. The differences in dyad and student numbers arise since a dyad was excluded from data analysis when one student met the criteria (thus was included) while his partner did not. | ||
| + | |||
| + | Due to technical difficulties during the test day, subject number in single post tests was further reduced: Server problems in one of the classrooms yielded significant differences between conditions in the amount of time to complete the post tests. To reduce these differences, we excluded students that had less than 10 minutes to solve the Cognitive Tutor post test (originally, 15 minutes were allocated to solve these tests). In the paper and pencil post test, we only included student data until the last question that was answered. Subsequent questions were counted as missing values. Since only few students were able to solve the last problem set, it is not reported in data analysis. | ||
| + | |||
| + | Since students’ prior knowledge, assessed as their grade in mathematics, had a positive influence on all learning outcome measures, it was included as covariate in data analysis. When results indicated an interaction between prior knowledge and condition (aptitude treatment interaction), we included the interaction term in the statistical model. | ||
| + | |||
| + | ''Collaborative [[normal post-test|retention]]'' | ||
| + | |||
| + | * ''[[error rate]]:'' no significant difference was found | ||
| + | * ''[[assistance score]]:'' We found indications for an aptitude treatment interaction in the assistance needed to solve the problems. The covariance analysis with interaction term yielded a marginally significant effect of condition, F(2,47) = 2.81, p = .07, η² = .11: In contrast to our hypothesis, dyads in the scripted condition had highest assistance scores. As indicated by the aptitude treatment interaction, the disadvantage of the scripted condition was mainly due to a detrimental learning outcome of students with low prior knowledge: for these students, it was particularly difficult to solve the problems when the script support was removed for the first time. | ||
| + | * ''elaboration time:'' Conditions significantly differed in the elaboration time, F(2,50) = 5.06, p = .01. Both collaborative conditions spent significantly more time elaborating after errors and hints than students in the individual condition, t(50) = 4.16, p = .00. | ||
| + | |||
| + | ''Individual [[normal post-test|retention]]'' | ||
| + | |||
| + | * No differences in ''[[error rate]]'' or ''[[assistance score]]'' were found, indicating that the temporary disadvantage of low prior knowledge students in the scripted condition was no longer existing. | ||
| + | * ''elaboration time:'' Conditions significantly differed in the elaboration time, F(2,90) = 3.59, p = .03. Again, both collaborative conditions spent significantly more time elaborating after errors and hints than students in the individual condition, t(47.26) = 1.98, p = .05. Furthermore, the elaboration time was higher in the scripted condition than in the unscripted condition, t(40.56) = 2.14, p = .04. The elaboration time was negatively associated with the assistance score (r = -.22, p = .04), indicating that the elaborative learning processes after errors and hints indeed reduced the assistance needed to solve the problems. | ||
| + | |||
| + | ''[[Transfer]]'' | ||
| + | |||
| + | * As in the pre study, the scripted condition showed highest test scores in every problem set of the transfer test (although differences did not reach significance for the 1st and 3rd problem set) | ||
| + | * Basic concepts, open format: | ||
| + | ** A marginally significant aptitude treatment interaction indicates that collaboration is particularly beneficial for students with low prior knowledge. | ||
| + | ** We found marginally significant differences between conditions, F(2,87) = 2.27, p = .11, η² = .05. Students who learned collaboratively were better at reasoning about mathematical concepts than students who learned on their own, p = .04. | ||
| + | |||
| + | ''[[Accelerated future learning|Future Learning]]'' | ||
| − | ''' | + | * ''[[error rate]]:'' We found significant differences between conditions in the error rate, F(2,54) = 5.46, p = .01, η² = .17. The collaboration script positively influenced students’ collaborative problem-solving of the new task format, t(54) = -2.07, p = .04 (scripted vs. unscripted condition). |
| + | * ''[[assistance score]]´:'' The pattern was similar with regard to the assistance score, although differences between conditions did not reach statistical significance, F(2,54) = 1.54, p = .22. | ||
| + | * ''elaboration time:'' No significant differences were found. Again, elaboration time was negatively associated with the assistance score (r = -.27, p = .04). | ||
| − | + | <br> | |
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | ! | ||
| + | ! individual | ||
| + | ! unscripted | ||
| + | ! scripted | ||
| + | |- | ||
| + | ! colspan="4" align = "center" | Collaborative Retention | ||
| + | |- | ||
| + | | Error Rate || align="right"| .36 || align="right"| .38 || align="right"| .41 | ||
| + | |- | ||
| + | | Assistance Score || align="right"| .93 || align="right"| .86 || align="right"| 1.10 | ||
| + | |- | ||
| + | | Elaboration Time || align="right"| 12.66 || align="right"| 17.63 || align="right"| 17.81 | ||
| + | |- | ||
| + | ! colspan="4" align = “center” | Individual Retention | ||
| + | |- | ||
| + | | Error Rate || align="right"| .36 || align="right"| .36 || align="right"| .35 | ||
| + | |- | ||
| + | | Assistance Score || align="right"| .97 || align="right"| .98 || align="right"| 1.01 | ||
| + | |- | ||
| + | | Elaboration Time || align="right"| 16.14 || align="right"| 17.57 || align="right"| 27.32 | ||
| + | |- | ||
| + | ! colspan="4" align = “center” | Future Learning | ||
| + | |- | ||
| + | | Error Rate || align="right"| .30 || align="right"| .44 || align="right"| .36 | ||
| + | |- | ||
| + | | Assistance Score || align="right"| 1.85 || align="right"| 2.73 || align="right"| 2.01 | ||
| + | |- | ||
| + | | Elaboration Time || align="right"| 10.97 || align="right"| 13.54 || align="right"| 13.56 | ||
| + | |- | ||
| + | ! colspan="4" align = “center” | Transfer | ||
| + | |- | ||
| + | | Basic Concepts: Discrete Answers || align="right"| 4.27 || align="right"| 4.17 || align="right"| 4.79 | ||
| + | |- | ||
| + | | Basic Concepts: Open Format || align="right"| 1.30 || align="right"| 1.73 || align="right"| 2.17 | ||
| + | |- | ||
| + | | System Concept: Discrete Answers || align="right"| 2.01 || align="right"| 1.94 || align="right"| 2.14 | ||
| + | |} | ||
| + | '''Table 2'''. Means of the Robust Learning Measures | ||
| + | <br>Note: for error rate, assistance score, and the variables of the transfer test, means are adjusted for differences in prior knowledge | ||
| + | <br> | ||
=== Explanation === | === Explanation === | ||
| − | This study is part of the [[Interactive_Communication|Interactive Communication cluster]], and its hypothesis is a specialization of the IC cluster’s central hypothesis. According to the IC cluster’s hypothesis, | + | This study is part of the [[Interactive_Communication|Interactive Communication cluster]], and its hypothesis is a specialization of the IC cluster’s central hypothesis. According to the IC cluster’s hypothesis, there are three possible reasons why an interactive treatment might be better. First, it might add new paths to the [[learning event space]] (e.g. the learning partner offers knowledge the other person lacks). Second, it might improve students’[[ path choice]]. And third, students might traverse the paths differently, e.g. by being more attentive, yielding to increased [[path effects]]. |
| − | + | These three mechanisms can also be found in this study: | |
| − | * ''Individual condition'': The existing Cognitive Tutor already offers | + | * ''Individual condition'': The existing [[Cognitive tutor|Cognitive Tutor]] already offers a rich [[learning event space]], providing immediate error feedback and enabling students to ask for help. However, students’ [[path choice]] isn’t always optimal, and they often could traverse the paths chosen more effectively. For instance, when they make an error or ask for a hint, students do not always use this learning opportunity effectively, reflect on their errors and hints and engage in [[sense making]] processes. |
| − | * ''Unscripted collaboration condition | + | * ''Unscripted collaboration condition'': By enhancing the [[Cognitive tutor|Algebra I Cognitive Tutor]] to be a [[collaborative learning environment]], we added a second learning resource – the learning partner. This adds further correct learning paths to the [[learning event space]], for instance, learning by giving explanations, the possibility to request help, and learning by knowledge co-construction. Furthermore, students have the opportunity to reflect on the [[conceptual knowledge|mathematical concepts]] in natural language interaction in order to gain a deeper understanding. However, similarly to the learning paths in an individual setting, students do not always capitalize on these learning opportunities. |
| − | * ''Scripted collaboration condition | + | * ''Scripted collaboration condition'': To increase the probability that students traverse the [[learning event space]] most effectively, students’ interaction in the scripted collaboration condition is guided by the [[Collaboration scripts|Collaborative Problem Solving Script]]. By prompting [[collaboration skill]]s that have shown to improve learning (i.e. impacting students’ [[path choice]]) and by guiding students’ interaction when meeting impasses (i.e. increasing the [[path effects]]), we expect students to engage in a more fruitful [[collaboration]] that yields [[robust learning]]. |
=== Annotated bibliography === | === Annotated bibliography === | ||
| − | * Rummel, N., Diziol, D., Spada, H., & McLaren, B. M. ( | + | * Diziol, D., Rummel, N., Kahrimanis, G., Guevara, T., Holz, J., Spada, H., & Fiotakis, G. (2008). Using contrasting cases to better understand the relationship between students’ interactions and their learning outcome. In G. Kanselaar, V. Jonker, P.A. Kirschner, & F. Prins, (Eds.), ''International perspectives of the learning sciences: Cre8ing a learning world. Proceedings of the Eighth International Conference of the Learning Sciences (ICLS 2008), Vol 3'' (pp. 348-349). International Society of the Learning Sciences, Inc. ISSN 1573-4552. |
| − | * Rummel, N., Spada, H., Diziol, D. ( | + | * Rummel, N., Diziol, D. & Spada, H. (2008). Analyzing the effects of scripted collaboration in a computer-supported learning environment by integrating multiple data sources. Paper presented at the ''Annual Conference of the American Educational Research Association'' (AERA-08). New York, NY, USA, March 2008. |
| − | * Diziol, D., Rummel, N., Spada, H., & McLaren, B. M. ( | + | * Diziol, D., Rummel, N. & Spada, H. (2007). Unterstützung von computervermitteltem kooperativem Lernen in Mathematik durch Strukturierung des Problemlöseprozesses und adaptive Hilfestellung. Paper presented at the ''11th Conference of the "Fachgruppe Pädagogische Psychologie der Deutschen Gesellschaft für Psychologie" [German Psychological Association]''. Humboldt Universität zu Berlin, September 2007. |
| − | * | + | * Rummel, N., Diziol, D. & Spada, H. (2007). Förderung mathematischer Kompetenz durch kooperatives Lernen: Erweiterung eines intelligenten Tutorensystems. Paper presented at the ''5th Conference of the "Fachgruppe Medienpsychologie der Deutschen Gesellschaft für Psychologie" [German Psychological Association]''. TU Dresden, September 2007. |
| − | * Rummel, N., Diziol, D., Spada, H., McLaren, B., Walker, E. & Koedinger, K. (2006) Flexible support for collaborative learning in the context of the Algebra I Cognitive Tutor. Workshop paper presented at the ''Seventh International Conference of the Learning Sciences'' (ICLS 2006). Bloomington, IN, USA. | + | * Rummel, N., Diziol, D., Spada, H., & McLaren, B. M. (2007). Scripting Collaborative Problem Solving with the Cognitive Tutor Algebra: A Way to Promote Learning in Mathematics. Paper presented at the ''European Association for Research on Learning and Instrution'' (EARLI-07). Budapest, August 28 - September 1, 2007. |
| − | + | * Rummel, N., Spada, H., Diziol, D. (2007). Evaluating Collaborative Extensions to the Cognitive Tutor Algebra in an In Vivo Experiment. Lessons Learned. Paper presented at the ''European Association for Research on Learning and Instrution'' (EARLI-07). Budapest, August 28 - September 1, 2007. | |
| + | * Diziol, D., Rummel, N., Spada, H., & McLaren, B. M. (2007). Promoting Learning in Mathematics: Script Support for Collaborative Problem Solving with the Cognitive Tutor Algebra. In C. A. Chinn, G. Erkens & S. Puntambekar (Eds.), ''Mice, minds and sociecty. Proceedings of the Computer Supported Collaborative Learning (CSCL) Conference 2007, Vol 8, I'' (pp. 39-41). International Society of the Learning Sciences, Inc. ISSN 1819-0146 [[http://www.learnlab.org/uploads/mypslc/publications/cscl07-diziolrummelspadamclaren.pdf pdf]] | ||
| + | * Rummel, N., Spada, H. & Diziol, D. (2007). Can collaborative extensions to the Algebra I Cognitive Tutor enhance robust learning? An in vivo experiment. Paper presented at the ''Annual Conference of the American Educational Research Association'' (AERA-07). Chicago, IL, USA, April 2007. | ||
| + | * Rummel, N., Diziol, D., Spada, H., McLaren, B., Walker, E. & Koedinger, K. (2006) Flexible support for collaborative learning in the context of the Algebra I Cognitive Tutor. Workshop paper presented at the ''Seventh International Conference of the Learning Sciences'' (ICLS 2006). Bloomington, IN, USA. [[http://learnlab.org/uploads/mypslc/publications/icls2006workshop_rummeletal.pdf pdf]] | ||
* Diziol, D. (2006). ''Development of a collaboration script to improve students` algebra learning when solving problems with the Algebra I, Cognitive Tutor.'' Diploma Thesis. Albert-Ludwigs-Universität Freiburg, Germany: Institute of Psychology, June 2006. | * Diziol, D. (2006). ''Development of a collaboration script to improve students` algebra learning when solving problems with the Algebra I, Cognitive Tutor.'' Diploma Thesis. Albert-Ludwigs-Universität Freiburg, Germany: Institute of Psychology, June 2006. | ||
| − | * McLaren, B., Rummel, N. and others (2005). Improving algebra learning and collaboration through collaborative extensions to the Algebra Cognitive Tutor. Poster presented at the ''Conference on Computer Supported Collaborative Learning'' (CSCL-05), May 2005, Taipei, Taiwan | + | * McLaren, B., Rummel, N. and others (2005). Improving algebra learning and collaboration through collaborative extensions to the Algebra Cognitive Tutor. Poster presented at the ''Conference on Computer Supported Collaborative Learning'' (CSCL-05), May 2005, Taipei, Taiwan. |
| − | |||
=== References === | === References === | ||
| + | * Aleven, V., McLaren, B.M., Roll, I., & Koedinger, K. R. (2004). Toward tutoring help seeking: Applying cognitive modelling to meta-cognitive skills. In J. C. Lester, R. M. Vicari & F. Paraguaçu (Eds.), ''Proceedings of Seventh International Conference on Intelligent Tutoring Systems, ITS 2004'' (pp. 227-239). Berlin: Springer. | ||
* Anderson, J. R., Corbett, A. T., Koedinger, K. R., & Pelletier, R. (1995). Cognitive tutors: Lessons learned. ''Journal of the Learning Sciences, 4''(2), 167-207. | * Anderson, J. R., Corbett, A. T., Koedinger, K. R., & Pelletier, R. (1995). Cognitive tutors: Lessons learned. ''Journal of the Learning Sciences, 4''(2), 167-207. | ||
| + | * Avouris, N., Fiotakis, G., Kahrimanis, G., Margaritis, M., & Komis, V. (2007) Beyond logging of fingertip actions: analysis of collaborative learning using multiple sources of data. ''Journal of Interactive Learning Research JILR, 18''(2), 231-250. | ||
| + | * Baker, R. S., Corbett, A. T., & Koedinger, K. R. (2004). ''Detecting student misuse of intelligent tutoring systems.'' Paper presented at the Proceedings of the 7th International Conference on Intelligent Tutoring Systems. | ||
* Berg, K. F. (1993). ''Structured cooperative learning and achievement in a high school mathematics class.'' Paper presented at the Annual Meeting of the American Educational Research Association, Atlanta, GA. | * Berg, K. F. (1993). ''Structured cooperative learning and achievement in a high school mathematics class.'' Paper presented at the Annual Meeting of the American Educational Research Association, Atlanta, GA. | ||
* Koedinger, K. R., Anderson, J. R., Hadley, W. H., & Mark, M. A. (1997). Intelligent tutoring goes to school in the big city. ''International Journal of Artificial Intelligence in Education, 8'', 30-43. | * Koedinger, K. R., Anderson, J. R., Hadley, W. H., & Mark, M. A. (1997). Intelligent tutoring goes to school in the big city. ''International Journal of Artificial Intelligence in Education, 8'', 30-43. | ||
* Kollar, I., Fischer, F., & Hesse, F. W. (in press). Collaboration scripts - a conceptual analysis. ''Educational Psychology Review''. | * Kollar, I., Fischer, F., & Hesse, F. W. (in press). Collaboration scripts - a conceptual analysis. ''Educational Psychology Review''. | ||
| − | * Meier, A., Spada, H. & Rummel, N. ( | + | * Meier, A., Spada, H. & Rummel, N. (2007). A rating scheme for assessing the quality of computer-supported collaboration processes. ''International Journal of Computer-Supported Collaborative Learning.'' published online first at DOI http://dx.doi.org/10.1007/s11412-006-9005-x, February 2007 |
* Rummel, N., & Spada, H. (2005). Learning to Collaborate: An Instructional Approach to Promoting Collaborative Problem Solving in Computer-Mediated Settings. ''Journal of the Learning Sciences, 14''(2), 201-241. | * Rummel, N., & Spada, H. (2005). Learning to Collaborate: An Instructional Approach to Promoting Collaborative Problem Solving in Computer-Mediated Settings. ''Journal of the Learning Sciences, 14''(2), 201-241. | ||
* Teasley, S. D. (1995). The role of talk in children's peer collaborations. ''Developmental Psychology, 31''(2), 207-220. | * Teasley, S. D. (1995). The role of talk in children's peer collaborations. ''Developmental Psychology, 31''(2), 207-220. | ||
| + | === Connections === | ||
| + | As this study, [[Walker A Peer Tutoring Addition]] adds scripted collaborative problem solving to the Cognitive Tutor Algebra. The studies differ in the way collaboration is integrated in the Tutor. First, in this study, both students first prepare one subtasks of a problem to mutually solve the complex story problem later on. Thus, although the students are experts for different parts of the problem, they have a comparable knowledge level during collaboration. In contrast, in Walker et al.'s study, one student prepares to teach his partner. Then, they change roles. Thus, during collaboration, their knowledge level differs. Second, in this study, collaboration was face to face, whereas the Walker et al. study used a chat tool for interaction. | ||
| + | |||
| + | Similar to the adaptive script component of the Collaborative Problem-Solving Script, the [[The Help Tutor Roll Aleven McLaren|Help Tutor project]] aims at improving students' [[help-seeking behavior]] and at reducing students' tendency to [[Gaming the system|game the system]]. <br> Furthermore, both studies contain instructions to teach [[metacognition]]. The metacognitive component in our study instructs students to monitor their interaction in order to improve it in subsequent collaborations; the Help Tutor project asks students to evaluate their need for help in order to improve their help-seeking behavior when learning on the Tutor. | ||
| + | |||
| + | Both in this study and in the [[Reflective Dialogues (Katz)|Reflective Dialogue study]] from Katz, students are asked to engage in reflection following each problem-solving. In this study, the reflection concentrates on the collaborative skills, while in Katz' study, the reflection concentrates on students' domain knowledge of the main principles applied in the problem. | ||
| + | |||
| + | Furthermore, both our study and the [[Help Lite (Aleven, Roll)]] aim at improving conceptual knowledge. | ||
| + | |||
| + | ==== Future plans ==== | ||
| + | Our future plans for January 2008 – June 2008: | ||
| + | * Paper publication (robust learning measures) | ||
| + | * Continue with the in-depth analysis of collaboration during learning phase (i.e. collaborative learning process) and during test phase, using contrasting case analysis | ||
| + | * Paper publication (interaction analysis of contrasting cases) | ||
| + | * Conference contributions in symposiums at AERA 2008 and ICLS 2008 | ||
| − | Study [[Category: | + | [[Category:Study]] |
| + | [[Category:Protected]] | ||
Latest revision as of 00:12, 16 December 2010
Contents
Collaborative Extensions to the Cognitive Tutor Algebra: Scripted Collaborative Problem Solving
Nikol Rummel, Dejana Diziol, Bruce M. McLaren, and Hans Spada
Summary Tables
| PIs | Bruce McLaren, Nikol Rummel & Hans Spada |
| Other Contributers |
|
Pre Study
| Study Start Date | 03/13/06 |
| Study End Date | 03/21/06 |
| LearnLab Site | CWCTC |
| LearnLab Course | Algebra |
| Number of Students | N = 30 |
| Average # of hours per participant | 3 hrs. |
| Data in DataShop | yes |
Full Study
| Study Start Date | 04/03/06 |
| Study End Date | 04/07/06 |
| LearnLab Site | CWCTC |
| LearnLab Course | Algebra |
| Number of Students | N = 139 |
| Average # of hours per participant | 3 hrs. |
| Data in DataShop | yes |
Abstract
In this project, the Algebra I Cognitive Tutor is extended to a collaborative learning environment: students learn to solve system of equations problems while working in dyads. As research has shown, collaborative problem solving and learning has the potential to increase elaboration on the learning content. However, students are not always able to effectively meet the challenges of a collaborative setting. To ensure that students capitalize on collaborative problem solving with the Tutor, a collaboration script was developed that guides their interaction and prompts fruitful collaboration. During the scripted problem solving, students alternate between individual and collaborative phases. Furthermore, they reflect on the quality of their interaction during a recapitulation phase that follows each problem they solve. During this phase, students self evaluate their interaction and plan how to improve it, thus they engage in metacognitive activities.
To assess the effectiveness of the script, we conducted two classroom studies. In an initial, small scale study (pre study) that served to establish basic effects and to test the procedure in a classroom setting, we compared scripted collaboration with an unscripted collaboration condition in which students collaborated without support. In the full study, we furthermore compared these collaborative conditions to an individual condition to assess the effect of the collaborative Tutor extension to regular Tutor use. The experimental learning phase took place on two days of instruction. On the third day, during the test phase, students completed several post tests that assessed robust learning. Results from the transfer test of the pre study revealed significant differences between conditions: Students that received script support during collaboration showed higher mathematical understanding and were better at reasoning about mathematical concepts. In the full study, results varied for the different measures of robust learning: While students of the scripted condition had a slight disadvantage when the script was removed for the first time (collaborative retention; note: only for students in the scripted condition, the problem-solving situation was different than during instruction), this disadvantage could no longer be found in the second retention test (individual retention). The transfer test revealed that students that learned collaboratively were better at reasoning about mathematical concepts. Finally, students of the scripted condition were better prepared for future learning situations than students that collaborated without script support.
Background and Significance
In our project, we combined two different instructional methods both of which have been shown to improve students’ learning in mathematics: Learning with intelligent tutoring systems (Koedinger, Anderson, Hadley, & Mark, 1997) and collaborative problem solving (Berg, 1993). The Cognitive Tutor Algebra that was used in our study is a tutor for mathematics instruction at the high school level. Students learn with the Tutor during part of the regular classroom sessions. The Tutor's main features are immediate error feedback, the possibility to ask for a hint when encountering impasses, and knowledge tracing, i.e. the Tutor creates and updates a model of the student’s knowledge and selects new problems tailored to the student’s knowledge level. Although several studies have proven its effectiveness, students do not always benefit from learning with the Tutor. First, because the Tutor places emphasis on learning procedural problem solving skills, yet a deep understanding of underlying mathematical concepts is not necessarily achieved (Anderson, Corbett, Koedinger, & Pelletier, 1995). Second, students do not always make good use of the learning opportunities provided by the Cognitive Tutor (e.g. help abuse, see Aleven, McLaren, Roll, & Koedinger, 2004; gaming the system, Baker, Corbett, & Koedinger, 2004). So far, the Cognitive Tutor has been used in an individual learning setting only. However, as research on collaborative learning has shown, collaboration can yield elaboration of learning content (Teasley, 1995), thus this could be a promising approach to reduce the Tutor’s shortcomings. On the other hand, students are not always able to effectively meet the challenges of a collaborative setting (Rummel & Spada, 2005). Collaboration scripts have proven effective in helping people meet the challenges encountered when learning or working collaboratively (Kollar, Fischer, & Hesse, in press). To ensure that students would profit from a collaboratively enhanced Tutor environment, we thus developed a collaboration script that prompts fruitful interaction on the Tutor while students learned to solve “systems of equations”, a content novel to the participating students. The script served two goals: First, to improve students’ robust learning of knowledge components relevant for the systems of equation units (i.e. both problem solving skills and understanding of the concepts). Second, students should increase their explicit knowledge of what constitutes a fruitful collaboration and improve their collaboration skills in subsequent interactions without further script support. This is particularly important due to the risk of overscripting collaboration that has been discussed in conjunction with scripting for longer periods of time (Rummel & Spada, 2005).
Glossary
See Scripted Collaborative Problem Solving Glossary
Research question
Does collaboration – and in particular scripted collaboration – improve students’ robust learning in the domain of algebra?
Does the script approach improve students’ collaboration, and does this result in more robust learning of the algebra content?
Independent variables
The independent variable was the mode of instruction. Three conditions were implemented in the learning phase that took place on two days of instruction:
- Individual condition: Students solved problems with the Algebra I Cognitive Tutor in the regular fashion (i.e. computer program as additional agent).
- Unscripted collaborative condition: Students solved problems on the Cognitive Tutor while working in dyads; thus, a second learning resource was added to the regular Tutor environment (i.e., both a peer and a computer program as additional agents).
- Scripted collaboration condition: As in the unscripted collaborative condition, students solved problems on the Tutor while working in dyads; however, their dyadic problem solving was guided by the Collaborative Problem-Solving Script (CPS) (i.e., both a peer and a computer program as additional agents; for an overview of the script structure, see Figure 1). Three script components supported their interaction in order to reach a more fruitful collaboration and improved learning:
- A fixed script component structured students’ collaboration in an individual and a collaborative phase (see Figure 1). During the individual phase, each student solved a single equation problem; during the collaborative phase, these problems were combined to a more complex system of equations problem. This division of expertise aimed at increasing the individual's responsibility for the common problem-solving process and thus at yielding a more fruitful interaction. In addition, the fixed script component structured the collaborative phase in several sub steps and prompted students to engage in elaborative interaction (see Figure 2 and 3).
- An adaptive script component provided prompts to improve the collaborative learning process when the dyad encountered difficulties in their problem solving. E.g., to prevent help abuse in the tutoring system and to stop students from proceeding in the hint sequence until reaching the bottom out hint, the dyad is prompted to elaborate on the Tutor hints when reaching the penultimate hint of the hint sequence (see Figure 4). This aims at enabling students to find the answer by themselves on basis of the help received and at students gaining knowledge to solve similar steps later on their own.
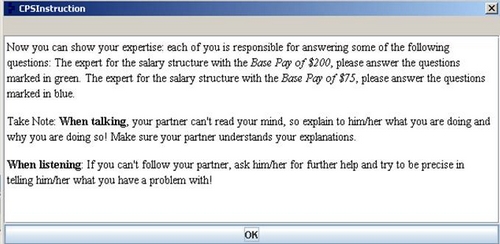
- A metacognitive script component prompted students to engage in reflection of the group process to improve their collaboration over subsequent interactions. Following each collaborative phase, students rated their interaction on 8 collaboration skills and set goals for the following collaboration. This phase was referred to as the "recapitulation phase"
Figure 1. Structure of the Collaborative Problem-Solving Script.
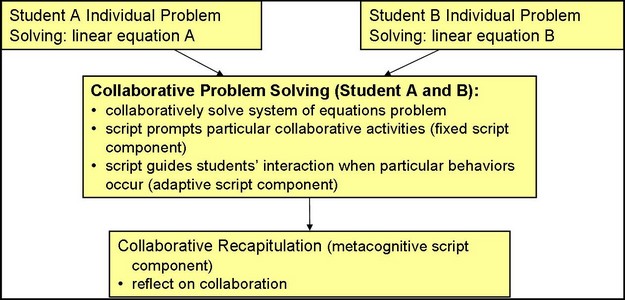
Figure 2 and 3. Screenshot of the enhanced Cognitive Tutor Algebra: Instructions for the following sub step (for details, see figure 3; responsibilities for student A and B marked by color of text.
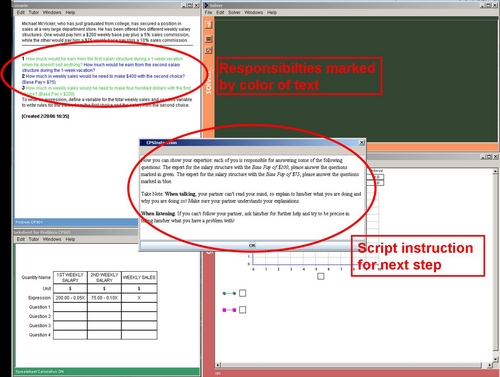
Figure 4. Adaptive script prompt: penultimate hint message (appeared when students clicked on "next hint" to reach the bottom-out hint).
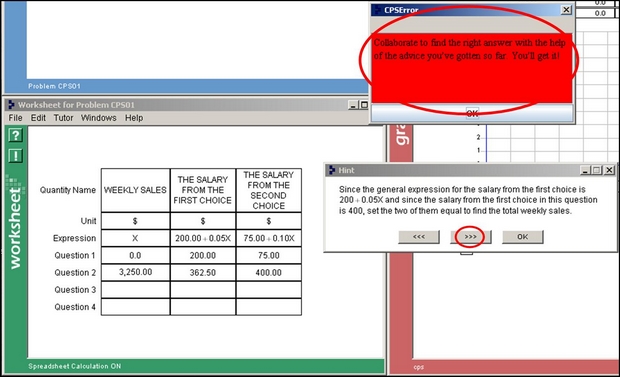
In all conditions, the Cognitive Tutor supported students’ problem solving by flagging their errors and by providing on-demand hints.
Communication between the collaborative partners in the collaborative conditions was face to face: they joined together at a single computer to solve the problems. In the scripted collaboration condition, the script structured the allocation of subtasks between the two students.
In the pre study that aimed at establishing basic effects and at testing the procedure in a classroom setting, we only compared unscripted and scripted collaborative problem solving.
Hypothesis
The hypothesis can be stated in two parts: knowledge gains in the domain of algebra and improvement of the dyads’ collaboration skills:
- We expect the collaborative conditions – in particular the scripted collaboration condition – to outperform the individual conditions in measures of robust learning of the algebra content.
- We expect that problem-solving with the Collaborative Problem-Solving Script will lead to a more effective interaction than unscripted collaboration in the learning phase. In addition, we expect that the newly gained collaboration skills will sustain during subsequent collaborations in the test phase when script support is no longer available.
Dependent variables
Students took several post tests during the test phase that took place two days after instruction:
- Normal post-test (retention): Two post-tests measured immediate retention. As during the learning phase, students solved system of equations problems on the Cognitive Tutor. The problems were “isomorphic” to those in the instruction, but had different content. One test was solved collaboratively to measure both students’ algebra skills and their collaboration skills, the other test was solved individually to assess if the students were able to generalize the gained knowledge to isomorphic problems when working on their own.
- Transfer: This paper and pencil test assessed students' understanding of the main mathematical concepts from the learning phase: slope, y-intercept and intersection point. The conceptual tasks students had to solve tapped the same knowledge components as the problems in instruction; however, the problems where non-isomorphic to those in the instruction, thus demanded students to flexibly apply their knowledge to problems with a new format. The test consisted of two problem sets with two different question formats: problem set 1 asked for the basic concepts y-intercept and slope, problem set 2 asked for the novel system’s concept of intersection point. Both sets were composed of questions with a distinct answer format and open format questions that asked students to explain their problem-solving.
- Accelerated future learning: To measure accelerated future learning, students learned how to solve problems in a new area of algebra – inequality problems. This test was administered on the Cognitive Tutor, thus students could ask the Tutor for hints and received immediate error feedback. According to their condition during the experimental learning phase, they either worked individually or collaboratively on this post test. However, in contrast to the learning phase, they did not receive additional instructions to support their collaboration.
Several variables from these post tests are compared to test the two hypotheses.
- For the post tests conducted on the Cognitive Tutor (retention and accelerated future learning), we extracted 3 variables from the Tutor logfiles.
- error rate
- assistance score
- the process variable elaboration time measures the average time spent after errors, bugs and hints. These are regarded as potential learning events: if students spend more time elaborating on their impasses, they can increase their knowledge and thus improve their problem-solving in subsequent problems. This variable was used as an indicator for deep learning processes during problem solving.
- For the paper and pencil post test (far transfer), we developed a scoring systems. For distinct format questions, students received 0 points for incorrect/missing answers and 1 point for correct answers; for open format questions , students received 0 points for incorrect, irrelevant or missing answers, 1 point for partly elaborated answers, and 2 points for fully elaborated answers. We summed points separately for the two question formats and the two problem sets of this post-test, resulting in four variables.
- To compare collaboration skills of students, we recorded students’ dialogues both during learning phase and during test phase. Based on the analysis method reported in Meier, Spada, and Rummel (2007), we developed a rating scheme that assesses students’ interaction from two different perspectives. With the first perspective, we evaluate the quality of their collaborative problem-solving, e.g. if they capitalize on the social resource and on the system resource to improve their learning. From the second perspective, we evaluate the quality of their interaction with dimensions such as “mathematical elaboration” and “dyad’s motivation”. We applied the rating scheme to our process data using ActivityLens (Avouris, Fiotakis, Kahrimanis, Margaritas, & Komis, 2007), a software tool that permits the integration of several data sources, in this case the integration of CTA log data and the audio and screen recordings from students' collaboration at the CTA.
These process analyses are part of an international collaboration with the research group of Nikos Avouris, University of Patras, Greece, in the context of the Kaleidoscope Network of Excellence project CAViCoLA (Computer-based Analysis and Visualization of Collaborative Learning Activites). Further information on these analyses can be found in Diziol et al. (paper accepted for presentation at the ICSL 2008, Utrecht).
Method
The study procedure took place during 3 classroom periods over the course of a week. During day 1 and day 2 (the learning phase), the experimental conditions (i.e. the independent variables) were implemented. On day 3, students had to solve several post-tests that assessed different aspects of robust learning.
Two in vivo classroom studies were conducted: a pre study with 3 classrooms, and a full study with 8 classrooms. The pre study aimed at establishing basic effects of the script and testing the procedure in a classroom setting, thus we only compared scripted to unscripted collaboration. In the full study, we compared the scripted collaboration condition to both an individual condition and an unscripted collaboration to evaluate the merits of both enhancing the Tutor with collaboration in general and scripted collaboration in particular. Due to the disruptiveness of students in the same class using different interventions, we used a between-class design.
Participants pre study:
The unscripted condition consisted of two classes (12 and 4 students), and the scripted condition consisted of one class (13 students). All classes were taught by the same teacher.
Participants full study:
- Individual condition: 1 class (21 students)
- Unscripted condition: 3 classes (18 + 16 + 16 dyads = 25 dyads)
- Scripted condition: 4 classes (16 + 16 + 18 + 18 dyads = 34 dyads)
Findings
The study was conducted at a vocational high school: Half a day, students took vocational classes (e.g. carpentry, cooking) and mathematics at the vocational school, half a day, they took the regular lessons at their home schools. This yielded a high rate of students’ absenteeism, and as a consequence, we had to exclude some dyads from further data analysis. We restricted the analysis to students that met the following criteria: they were present at least during one day of instruction, they were present at the test day, and they always worked according to their condition when present. For instance, a student from one of the collaborative conditions that worked individually on one day was excluded from further data analysis. The resulting participant numbers for data analysis in the two studies are reported in the respective findings sections.
Findings pre study:
In the pre study, nine students from the unscripted and ten students from the scripted condition met the criteria to be included in the data analysis. Since the subject number in the collaborative post tests is rather small, we’ll concentrate on the results of the paper and pencil post test (far transfer) that was solved individually. This test revealed substantial differences between conditions.
Significant differences were found both in the MANOVA (Pillai-Spur, F(4, 14) = 7.35, p < .05) and in subsequent ANOVAs. Multiple choice answers on basic concepts did not show a significant difference, F(1,17) = 2.26, ns. However, the scripted condition outperformed the unscripted condition on the discrete answer questions about the system’s concept, F(1,17) = 22.16, p < .01. A significant difference between conditions was also found for the open format questions of both problem sets with F(1,17) = 5.85, p < .05 for the basic concepts and F(1,17) = 17.01, p < .01 for the system’s concept. Particularly the results of the open format questions demonstrate the script’s effect on conceptual knowledge acquisition: after scripted interaction during the learning phase, students were better at articulating their mathematical thinking compared to their unscripted counterparts. However, it should be noted that in general students in both conditions had difficulties providing explanations, thus only reached low scores in the open format questions. The amount of wrong explanations and the number of students who did not even try to articulate their thinking was very high.
Findings full study:
In the full study, 17 students from the individual condition, 19 dyads (40 students) from the unscripted condition and 23 dyads (49 students) from the scripted condition were included in data analysis. The differences in dyad and student numbers arise since a dyad was excluded from data analysis when one student met the criteria (thus was included) while his partner did not.
Due to technical difficulties during the test day, subject number in single post tests was further reduced: Server problems in one of the classrooms yielded significant differences between conditions in the amount of time to complete the post tests. To reduce these differences, we excluded students that had less than 10 minutes to solve the Cognitive Tutor post test (originally, 15 minutes were allocated to solve these tests). In the paper and pencil post test, we only included student data until the last question that was answered. Subsequent questions were counted as missing values. Since only few students were able to solve the last problem set, it is not reported in data analysis.
Since students’ prior knowledge, assessed as their grade in mathematics, had a positive influence on all learning outcome measures, it was included as covariate in data analysis. When results indicated an interaction between prior knowledge and condition (aptitude treatment interaction), we included the interaction term in the statistical model.
Collaborative retention
- error rate: no significant difference was found
- assistance score: We found indications for an aptitude treatment interaction in the assistance needed to solve the problems. The covariance analysis with interaction term yielded a marginally significant effect of condition, F(2,47) = 2.81, p = .07, η² = .11: In contrast to our hypothesis, dyads in the scripted condition had highest assistance scores. As indicated by the aptitude treatment interaction, the disadvantage of the scripted condition was mainly due to a detrimental learning outcome of students with low prior knowledge: for these students, it was particularly difficult to solve the problems when the script support was removed for the first time.
- elaboration time: Conditions significantly differed in the elaboration time, F(2,50) = 5.06, p = .01. Both collaborative conditions spent significantly more time elaborating after errors and hints than students in the individual condition, t(50) = 4.16, p = .00.
Individual retention
- No differences in error rate or assistance score were found, indicating that the temporary disadvantage of low prior knowledge students in the scripted condition was no longer existing.
- elaboration time: Conditions significantly differed in the elaboration time, F(2,90) = 3.59, p = .03. Again, both collaborative conditions spent significantly more time elaborating after errors and hints than students in the individual condition, t(47.26) = 1.98, p = .05. Furthermore, the elaboration time was higher in the scripted condition than in the unscripted condition, t(40.56) = 2.14, p = .04. The elaboration time was negatively associated with the assistance score (r = -.22, p = .04), indicating that the elaborative learning processes after errors and hints indeed reduced the assistance needed to solve the problems.
- As in the pre study, the scripted condition showed highest test scores in every problem set of the transfer test (although differences did not reach significance for the 1st and 3rd problem set)
- Basic concepts, open format:
- A marginally significant aptitude treatment interaction indicates that collaboration is particularly beneficial for students with low prior knowledge.
- We found marginally significant differences between conditions, F(2,87) = 2.27, p = .11, η² = .05. Students who learned collaboratively were better at reasoning about mathematical concepts than students who learned on their own, p = .04.
- error rate: We found significant differences between conditions in the error rate, F(2,54) = 5.46, p = .01, η² = .17. The collaboration script positively influenced students’ collaborative problem-solving of the new task format, t(54) = -2.07, p = .04 (scripted vs. unscripted condition).
- assistance score´: The pattern was similar with regard to the assistance score, although differences between conditions did not reach statistical significance, F(2,54) = 1.54, p = .22.
- elaboration time: No significant differences were found. Again, elaboration time was negatively associated with the assistance score (r = -.27, p = .04).
| individual | unscripted | scripted | |
|---|---|---|---|
| Collaborative Retention | |||
| Error Rate | .36 | .38 | .41 |
| Assistance Score | .93 | .86 | 1.10 |
| Elaboration Time | 12.66 | 17.63 | 17.81 |
| Individual Retention | |||
| Error Rate | .36 | .36 | .35 |
| Assistance Score | .97 | .98 | 1.01 |
| Elaboration Time | 16.14 | 17.57 | 27.32 |
| Future Learning | |||
| Error Rate | .30 | .44 | .36 |
| Assistance Score | 1.85 | 2.73 | 2.01 |
| Elaboration Time | 10.97 | 13.54 | 13.56 |
| Transfer | |||
| Basic Concepts: Discrete Answers | 4.27 | 4.17 | 4.79 |
| Basic Concepts: Open Format | 1.30 | 1.73 | 2.17 |
| System Concept: Discrete Answers | 2.01 | 1.94 | 2.14 |
Table 2. Means of the Robust Learning Measures
Note: for error rate, assistance score, and the variables of the transfer test, means are adjusted for differences in prior knowledge
Explanation
This study is part of the Interactive Communication cluster, and its hypothesis is a specialization of the IC cluster’s central hypothesis. According to the IC cluster’s hypothesis, there are three possible reasons why an interactive treatment might be better. First, it might add new paths to the learning event space (e.g. the learning partner offers knowledge the other person lacks). Second, it might improve students’path choice. And third, students might traverse the paths differently, e.g. by being more attentive, yielding to increased path effects.
These three mechanisms can also be found in this study:
- Individual condition: The existing Cognitive Tutor already offers a rich learning event space, providing immediate error feedback and enabling students to ask for help. However, students’ path choice isn’t always optimal, and they often could traverse the paths chosen more effectively. For instance, when they make an error or ask for a hint, students do not always use this learning opportunity effectively, reflect on their errors and hints and engage in sense making processes.
- Unscripted collaboration condition: By enhancing the Algebra I Cognitive Tutor to be a collaborative learning environment, we added a second learning resource – the learning partner. This adds further correct learning paths to the learning event space, for instance, learning by giving explanations, the possibility to request help, and learning by knowledge co-construction. Furthermore, students have the opportunity to reflect on the mathematical concepts in natural language interaction in order to gain a deeper understanding. However, similarly to the learning paths in an individual setting, students do not always capitalize on these learning opportunities.
- Scripted collaboration condition: To increase the probability that students traverse the learning event space most effectively, students’ interaction in the scripted collaboration condition is guided by the Collaborative Problem Solving Script. By prompting collaboration skills that have shown to improve learning (i.e. impacting students’ path choice) and by guiding students’ interaction when meeting impasses (i.e. increasing the path effects), we expect students to engage in a more fruitful collaboration that yields robust learning.
Annotated bibliography
- Diziol, D., Rummel, N., Kahrimanis, G., Guevara, T., Holz, J., Spada, H., & Fiotakis, G. (2008). Using contrasting cases to better understand the relationship between students’ interactions and their learning outcome. In G. Kanselaar, V. Jonker, P.A. Kirschner, & F. Prins, (Eds.), International perspectives of the learning sciences: Cre8ing a learning world. Proceedings of the Eighth International Conference of the Learning Sciences (ICLS 2008), Vol 3 (pp. 348-349). International Society of the Learning Sciences, Inc. ISSN 1573-4552.
- Rummel, N., Diziol, D. & Spada, H. (2008). Analyzing the effects of scripted collaboration in a computer-supported learning environment by integrating multiple data sources. Paper presented at the Annual Conference of the American Educational Research Association (AERA-08). New York, NY, USA, March 2008.
- Diziol, D., Rummel, N. & Spada, H. (2007). Unterstützung von computervermitteltem kooperativem Lernen in Mathematik durch Strukturierung des Problemlöseprozesses und adaptive Hilfestellung. Paper presented at the 11th Conference of the "Fachgruppe Pädagogische Psychologie der Deutschen Gesellschaft für Psychologie" [German Psychological Association]. Humboldt Universität zu Berlin, September 2007.
- Rummel, N., Diziol, D. & Spada, H. (2007). Förderung mathematischer Kompetenz durch kooperatives Lernen: Erweiterung eines intelligenten Tutorensystems. Paper presented at the 5th Conference of the "Fachgruppe Medienpsychologie der Deutschen Gesellschaft für Psychologie" [German Psychological Association]. TU Dresden, September 2007.
- Rummel, N., Diziol, D., Spada, H., & McLaren, B. M. (2007). Scripting Collaborative Problem Solving with the Cognitive Tutor Algebra: A Way to Promote Learning in Mathematics. Paper presented at the European Association for Research on Learning and Instrution (EARLI-07). Budapest, August 28 - September 1, 2007.
- Rummel, N., Spada, H., Diziol, D. (2007). Evaluating Collaborative Extensions to the Cognitive Tutor Algebra in an In Vivo Experiment. Lessons Learned. Paper presented at the European Association for Research on Learning and Instrution (EARLI-07). Budapest, August 28 - September 1, 2007.
- Diziol, D., Rummel, N., Spada, H., & McLaren, B. M. (2007). Promoting Learning in Mathematics: Script Support for Collaborative Problem Solving with the Cognitive Tutor Algebra. In C. A. Chinn, G. Erkens & S. Puntambekar (Eds.), Mice, minds and sociecty. Proceedings of the Computer Supported Collaborative Learning (CSCL) Conference 2007, Vol 8, I (pp. 39-41). International Society of the Learning Sciences, Inc. ISSN 1819-0146 [pdf]
- Rummel, N., Spada, H. & Diziol, D. (2007). Can collaborative extensions to the Algebra I Cognitive Tutor enhance robust learning? An in vivo experiment. Paper presented at the Annual Conference of the American Educational Research Association (AERA-07). Chicago, IL, USA, April 2007.
- Rummel, N., Diziol, D., Spada, H., McLaren, B., Walker, E. & Koedinger, K. (2006) Flexible support for collaborative learning in the context of the Algebra I Cognitive Tutor. Workshop paper presented at the Seventh International Conference of the Learning Sciences (ICLS 2006). Bloomington, IN, USA. [pdf]
- Diziol, D. (2006). Development of a collaboration script to improve students` algebra learning when solving problems with the Algebra I, Cognitive Tutor. Diploma Thesis. Albert-Ludwigs-Universität Freiburg, Germany: Institute of Psychology, June 2006.
- McLaren, B., Rummel, N. and others (2005). Improving algebra learning and collaboration through collaborative extensions to the Algebra Cognitive Tutor. Poster presented at the Conference on Computer Supported Collaborative Learning (CSCL-05), May 2005, Taipei, Taiwan.
References
- Aleven, V., McLaren, B.M., Roll, I., & Koedinger, K. R. (2004). Toward tutoring help seeking: Applying cognitive modelling to meta-cognitive skills. In J. C. Lester, R. M. Vicari & F. Paraguaçu (Eds.), Proceedings of Seventh International Conference on Intelligent Tutoring Systems, ITS 2004 (pp. 227-239). Berlin: Springer.
- Anderson, J. R., Corbett, A. T., Koedinger, K. R., & Pelletier, R. (1995). Cognitive tutors: Lessons learned. Journal of the Learning Sciences, 4(2), 167-207.
- Avouris, N., Fiotakis, G., Kahrimanis, G., Margaritis, M., & Komis, V. (2007) Beyond logging of fingertip actions: analysis of collaborative learning using multiple sources of data. Journal of Interactive Learning Research JILR, 18(2), 231-250.
- Baker, R. S., Corbett, A. T., & Koedinger, K. R. (2004). Detecting student misuse of intelligent tutoring systems. Paper presented at the Proceedings of the 7th International Conference on Intelligent Tutoring Systems.
- Berg, K. F. (1993). Structured cooperative learning and achievement in a high school mathematics class. Paper presented at the Annual Meeting of the American Educational Research Association, Atlanta, GA.
- Koedinger, K. R., Anderson, J. R., Hadley, W. H., & Mark, M. A. (1997). Intelligent tutoring goes to school in the big city. International Journal of Artificial Intelligence in Education, 8, 30-43.
- Kollar, I., Fischer, F., & Hesse, F. W. (in press). Collaboration scripts - a conceptual analysis. Educational Psychology Review.
- Meier, A., Spada, H. & Rummel, N. (2007). A rating scheme for assessing the quality of computer-supported collaboration processes. International Journal of Computer-Supported Collaborative Learning. published online first at DOI http://dx.doi.org/10.1007/s11412-006-9005-x, February 2007
- Rummel, N., & Spada, H. (2005). Learning to Collaborate: An Instructional Approach to Promoting Collaborative Problem Solving in Computer-Mediated Settings. Journal of the Learning Sciences, 14(2), 201-241.
- Teasley, S. D. (1995). The role of talk in children's peer collaborations. Developmental Psychology, 31(2), 207-220.
Connections
As this study, Walker A Peer Tutoring Addition adds scripted collaborative problem solving to the Cognitive Tutor Algebra. The studies differ in the way collaboration is integrated in the Tutor. First, in this study, both students first prepare one subtasks of a problem to mutually solve the complex story problem later on. Thus, although the students are experts for different parts of the problem, they have a comparable knowledge level during collaboration. In contrast, in Walker et al.'s study, one student prepares to teach his partner. Then, they change roles. Thus, during collaboration, their knowledge level differs. Second, in this study, collaboration was face to face, whereas the Walker et al. study used a chat tool for interaction.
Similar to the adaptive script component of the Collaborative Problem-Solving Script, the Help Tutor project aims at improving students' help-seeking behavior and at reducing students' tendency to game the system.
Furthermore, both studies contain instructions to teach metacognition. The metacognitive component in our study instructs students to monitor their interaction in order to improve it in subsequent collaborations; the Help Tutor project asks students to evaluate their need for help in order to improve their help-seeking behavior when learning on the Tutor.
Both in this study and in the Reflective Dialogue study from Katz, students are asked to engage in reflection following each problem-solving. In this study, the reflection concentrates on the collaborative skills, while in Katz' study, the reflection concentrates on students' domain knowledge of the main principles applied in the problem.
Furthermore, both our study and the Help Lite (Aleven, Roll) aim at improving conceptual knowledge.
Future plans
Our future plans for January 2008 – June 2008:
- Paper publication (robust learning measures)
- Continue with the in-depth analysis of collaboration during learning phase (i.e. collaborative learning process) and during test phase, using contrasting case analysis
- Paper publication (interaction analysis of contrasting cases)
- Conference contributions in symposiums at AERA 2008 and ICLS 2008