Visual-Verbal Learning (Aleven & Butcher Project)

Learning with Diagrams in Geometry: Strategic Support for Robust Learning

Vincent Aleven & Kirsten Butcher

Abstract

Does integration of visual and verbal knowledge during learning support deep understanding? Can student interactions with visual information during problem-solving support robust learning? The overall goal of this project is to gain a better understanding of 1) visual and verbal knowledge components in a problem-solving environment and, 2) how interacting with visual information can support the development of deep understanding. Ultimately, we are interested in coordination and integration processes in learning with visual and verbal knowledge components, and how these processes may support robust learning.

We are using the Geometry Cognitive Tutor as a research vehicle for our project. In geometry, visual information is represented in a problem diagram and verbal/symbolic information is represented in text that contains given and goal information as well as in conceptual rules/principles of geometry. The goals of this research are to investigate how coordination between and integration of visual and verbal information influence robust learning processes, as measured by knowledge retention and transfer. By coordination, we mean the processes that support mapping between relevant visual and verbal information as well as the processes that keep relevant knowledge components active. For example, in geometry a student needs to map between text references to angles and their location in a diagram and will need to maintain the numerical (given or solved) value of that angle to use in problem solving. By integration, we mean knowledge construction events that involve both visual and verbal knowledge components. For example, in geometry a student may need to construct an understanding of linear angles that includes both a verbal definition (e.g., “two adjacent angles that form a line”) and a visual situation description (e.g., a visual representation of the two angles formed by intersection of a line).

Glossary

See Visual-Verbal Learning Project Glossary

Research questions

1. Do students learn more with contiguous representations that support direct students' interaction and reasoning with diagrams? Is a contiguous representation sufficient to support integration of visual and verbal knowledge components?
2. Do students learn more when they produce elaborated explanations that connect visual and verbal knowledge components in geometry?
3. What robust learning processes are affected by contiguous representations and elaborated explanations during problem-solving?

Background & Significance

In this research, we draw upon previous work in learning with multimedia sources, self-explanations, and Cognitive Tutors. We hypothesize that two key cognitive processes support integrated knowledge development and robust learning when using visual and verbal representations. These processes are: 1) Successful mapping between visual and verbal information, and 2) Integration processes that combine visual and verbal representations into integrated knowledge components. We test the influence of these processes using three experimental factors: 1) contiguity, 2) elaborated explanations, and 3) integrated hint sequences.

By contiguity we mean placing related representations such as a table and a diagram in close proximity or even eliminating one of them altogether. Previous research in multimedia learning (e.g., Mayer, 2001) has identified learning benefits when visual and verbal information is placed is close temporal and spatial proximity; these benefits have been hypothesized to result from the easing of cognitive load required for mapping between visual and verbal information. Although we predict that contiguous representations may be useful during geometry learning, we believe that contiguous presentations alone may not be sufficient to promote the kinds of cognitive processes necessary for robust learning with visual and verbal information. Ultimately, we believe that scaffolds that support active integration of visual and verbal knowledge components will show the strongest effects in supporting robust learning.

Thus, the other two factors (elaborated explanations and integrated hints) are hypothesized to support processes of integration for visual and verbal knowledge components. Further, we hypothesize this integration as critical robust learning with multimedia sources.

By elaborated explanations we mean justifications given by the student of their problem-solving steps in which they elaborate not only which problem-solving principle is being applied (as investigated in much previous research on self-explanation with interactive learning environments) but also how it applies. A rich body of prior research has demonstrated that students develop deeper understanding of instructional materials when they self-explain to themselves during learning (e.g., Bielaczyc, Pirolli, & Brown, 1995; Chi, Bassok, Lewis, Reimann, & Glaser, 1989; Chi, de Leeuw, Chiu, & LaVancher, 1994). An existing version of the Geometry Cognitive Tutor implements student self-explanations of their problem solving using a very simple process: after correctly answering a geometry problem step, students must select the geometry rule or theorem that justifies their answer from a glossary menu of terms. Despite the limitations of the menu-based explanations, they have been shown to promote student learning in the Geometry Cognitive Tutor (Aleven & Koedinger, 2002). Thus, our question is whether more explicit forms of communication that link verbal and visual knowledge components can be more successful at promoting robust learning. We argue that scaffolds that promote sense making using both visual and verbal knowledge may be of greater benefit to students than scaffolds that require student explanations using only verbal declarative knowledge.

By integrated hints we mean instructional hint sequences that use visual means to highlight relations between visual information in the problem diagram and verbal information in the hint message. Previous research has shown that integrated representations can be useful for learning (e.g., Sweller & Chandler, 1994). Integrated hints may support robust learning better than verbal hints alone because they both the effort required for visual-verbal mapping, and they may support active integration of knowledge.

Dependent variables

• Pretest, normal post-test, and immediate transfer test measuring student performance on:
  • Problem-solving items isomorphic to the practiced problems (near-term knowledge retention)
  • Problem-solving items unlike those seen during problem practice (near-term knowledge transfer)
• Delayed posttest, measuring student performance on:
  • Problem-solving items isomorphic to the practiced problems (far-term knowledge retention)
  • Problem-solving items unlike those seen during problem practice (far-term knowledge transfer)
• Log data collected during tutor use, used to assess:
  • Learning curves
  • Time on task
  • Error rates
  • Latency of responses

Independent Variables

1. Contiguity of Representation

Contiguous representation (students work in diagram) vs. Non-contiguous representation (students work in separate table)

Figure 1. Noncontiguous representation: Screen shot of tutor interface.

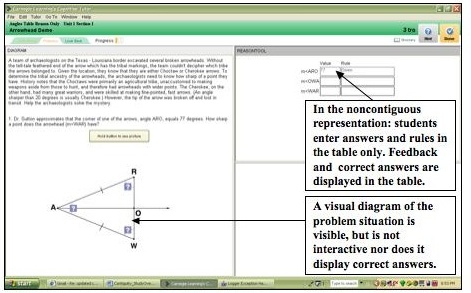
Figure 2. Contiguous representation: Screen shot of tutor interface.

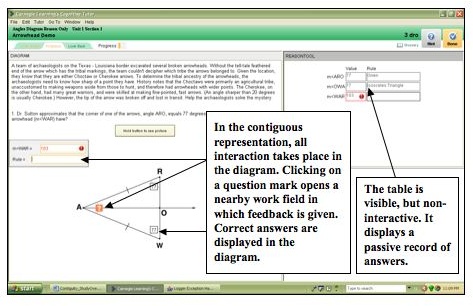
2. Type of Explanation

Verbal explanations (students state geometry principles only) vs. Elaborated Explanations (students state geometry principles and their application to the diagram)

3. Type of Hints

Verbal hints (hints provided as text only) vs. Integrated Hints (hints provided as text embedded in and applied to a diagram)

Hypotheses

• Contiguous representations in geometry decrease cognitive load (by supporting mapping) and increase strategic inferences during problem-solving, thus supporting immediate and long-term knowledge retention as well as transfer.
• Elaborated explanations promote integration of visual and verbal knowledge components during problem-solving, thus supporting knowledge transfer.
• Integrated hints promote sense making by promoting coordination through self-explanation and contiguity, thus supporting knowledge transfer.

Findings

Current findings suggest that interaction with visual representations during problem-solving supports deep transfer during learning. However, problem-solving performance is also supported by integrated self-explanations where students justify their problem solving steps with both verbal reasons (geometry rules) and visual information (diagram features relevant to the named geometry rule). Thus, integration may be supported by materials or explanations that support processing of visual and verbal information during learning.

Study 1 (In Vivo, Geometry Cognitive Tutor)

• Summary
  • In Vivo Study: 10th grade geometry classes in rural Pennsylvannia school
  • Domain: Angles curriculum in the Geometry Cognitive Tutor
  • Grade-matched pairs of students were randomly assigned to one of two conditions:
    • Diagram (Contiguous) Condition: Students interacted directly with geometry diagrams and accepted answers are displayed directly in the diagram
    • Table (Noncontiguous) Condition: Students work separate from the diagrams, in a distally located table

• Findings
  • No overall effect of experimental condition on students' performance on geometry answers or reasons at posttest
  • Although working in the Diagram condition improved lower-knowledge students' explanations at posttest, higher-knowledge students performed best when working in the Table condition. The result was evidenced by a significant 3-way interaction of Test Time (Pre- vs. Posttest) X Condition (Table vs. Diagram) X Prior Knowledge (Higher vs. Lower) for students' performance on geometry rules at posttest (F(1,39) = 6.2, p < .02).

Study 2 (In Vivo, Geometry Cognitive Tutor)

• Summary
  • In Vivo Study: 10th grade geometry classes in rural Pennsylvannia school
  • Domain: Circles curriculum in the Geometry Cognitive Tutor
  • Assessment was expanded to include not only answers and explanations for problem-solving items (as in Study 1), but also explanations on deep transfer items (explanations of unsolvable problems) and non-numerical reasoning items (true/false items that require students to judge whether a geometry rule is appropriate to relate named diagram elements).
  • Grade-matched pairs of students were randomly assigned to one of two conditions:
    • Diagram (Contiguous) Condition: Students interacted directly with geometry diagrams and accepted answers are displayed directly in the diagram
    • Table (Noncontiguous) Condition: Students work separate from the diagrams, in a distally located table

• Findings
  • Problem-solving: No condition differences for numerical answers (F(1, 89) = 1.03, p > .3) or explanations for solvable problems (F(1, 89) <1).
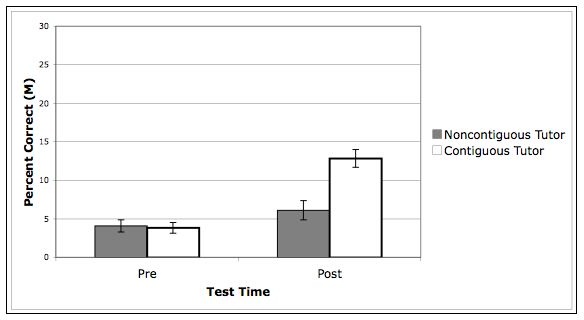
  • Deep Transfer Explanations: There was a significant effect of condition on students' explanations of unsolvable problems (F(1, 89) = 4.1, p = .046). Students in the Diagram (Contiguous) condition explained unsolvable problems better (M = .13, SE = .03) than students in the Table (Noncontiguous) condition (M = .06, SE = .02).

Figure 3. Mean performance on explanations for unsolvable problems by experimental condition, at pre- and posttest.

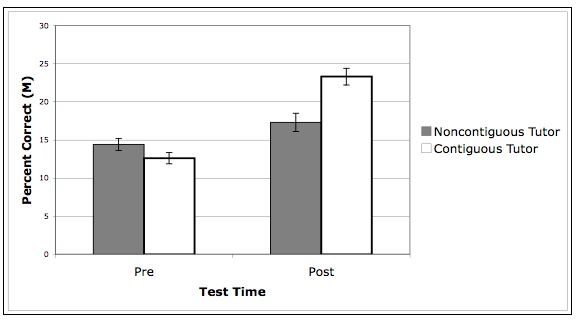
• • True/False items: Although there were no condition difference for performance on "true" items (F(1,89) = 2.4, p = .13), students in the Diagram (Contiguous) condition better recognized and explained false answers at posttest (F (1, 89) = 4.3, p = .04). That is, students from both conditions were equally able to recognize statements that gave valid relationships between geometry rules and diagram elements (Diagram, M = .71, SE = .04; Table, M = .72, SE = .03). However, students who interacted with diagrams during practice were better able to recognize when and explain why given geometry rules were inappropriate to relate named diagram elements (M = .23, SE = .02) than students who worked separately from diagrams during practice (M = .17, SE = .02).

Figure 4. Mean performance on recognizing/explaining inappropriate applications of geometry rules, by experimental condition at pre- and posttest.

Study 3 (In Vivo, Paper-based Difficulty Factors Analysis)

• Summary
  • In Vivo Study: 10th grade geometry classes in rural Pennsylvannia school
  • Format: Paper-based Difficulty Factors Analysis (DFA) covering Angles content from the Geometry Cognitive Tutor
  • Problems varied along two dimensions:
    • Problem Format: Diagram vs. Table. In Diagram-format problems, students entered answers within the geometry diagram. In the Table format, students entered answers in a table separate from the geometry diagram.
    • Explanation Type: Simple vs. Elaborated Explanations. Simple explanations required students to name only the geometry rule that justified their problem-solving steps. Elaborated explanations required students to name the geometry rule and the known diagram elements that allowed them to use the rule for each problem-solving step.
  • Students using the standard version of the Geometry Cognitive Tutor took the paper-based DFA test midway through their completion of the Angles unit on the tutor.

• Findings
  • Although there is an overall trend that, with no practice, students perform best in the familiar Table format (F (1, 88) = 3.47, p = .07), the type of explanations required significantly impacted performance (F (1, 88), = 6.75, p = .01). Students performed better on problem-solving when required to provide elaborated explanations (M = 42., SE = .04) compared to when they produced only simple, rule-based explanations (M = .34, SE = .04).

Explanation

Contiguous representations may support mapping between visual and verbal information in problem-solving. However, the deep transfer effects seen in Experiment 2 suggest that contiguous representations may help students integrate visual and verbal knowledge components during learning. In PSLC terms, the contiguous representations reduce the effort of deep learning paths in the learning event space (by supporting strategic inferences and reasoning directly with the diagram). Our data may also suggest that contiguous representations can have a learning path effect: students who are able to reason directly with diagram representations may attend more closely to the geometric features and relations to which geometry principles apply. This could impact meaningful learning by increasing feature validity of the visual and verbal knowledge components.

Data analysis is currently underway for a completed in-vivo study that tested elaborated explanations in addition to the effect of contiguity. In-vivo study of integrated hint sequences is planned for Spring 2007. We have evidence from the (paper-based) difficulty factors analysis that elaborated explanations support problem solving performance. We hypothesize that integrated hints also will support robust learning. Both of these manipulations, elaborated explanations and integrated hints, support coordination through self-explanation of visual and verbal information. Providing these multiple representations during learning likely affects path choice. For example, when students are required to explain the application of geometry principles using diagrams, there will be only small differences in estimated effort of shallow and deep strategies since shallow strategies are unlikely to achieve the correct answer. Further, we anticipate that elaborated explanations and integrated hints also produce path effects: the processes that students employ via path choice are more effective when the materials support use of visual and verbal information during sense making. Specifically, scaffolds or materials that support sense making with visual and verbal information should promote integration.

Annotated Bibliography

• Presentation to the PSLC Advisory Board, Fall 2006. Link to Powerpoint slides
• Butcher, K. B., & Aleven, V. A. (submitted). Integrating Visual and Verbal Knowledge During Classroom Learning with Computer Tutors. Paper submitted to Cognitive Science 2007 Conference.

References

• Bielaczyc, K., Pirolli, P. L., & Brown, A. L. (1995). Training in self-explanation and self-regulation strategies: Investigating the effects of knowledge acquisition activities on problem solving. Cognition & Instruction, 13, 221-252.
• Chi, M. T., Bassok, M., Lewis, M. W., Reimann, P., & Glaser, R. (1989). Self-explanations: How students study and use examples in learning to solve problems. Cognitive Science, 13, 145-182.
• Chi, M. T. H., de Leeuw, N., Chiu, M.-H., & LaVancher, C. (1994). Eliciting self-explanations improves understanding. Cognitive Science, 18, 439-477.
• Koedinger, K. R., & Anderson, J. R. (1990). Abstract planning and perceptual chunks: Elements of expertise in geometry. Cognitive Science, 14, 511-550.
• Lovett, M. C., & Anderson, J. R. (1994). Effects of solving related proofs on memory and transfer in geometry problem solving. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20, 366-378.
• Mayer, R. E. (2001). Multimedia Learning. Cambridge, Cambridge University Press.
• Sweller, J., & Chandler, P. (1994). Why some material is difficult to learn. Cognition and Instruction, 12, 185-233.