Baker Choices in LE Space

How Content and Interface Features Influence Student Choices Within the Learning Spaces

Ryan S.J.d. Baker, Albert T. Corbett, Kenneth R. Koedinger, Ma. Mercedes T. Rodrigo

Overview

PIs: Ryan S.J.d Baker

Co-PIs: Albert T. Corbett, Kenneth R. Koedinger

Others who have contributed 160 hours or more:

• Jay Raspat, Carnegie Mellon University, taxonomy development
• Adriana M.J.A. de Carvalho, Carnegie Mellon University, data coding

Others significant personnel :

• Ma. Mercedes T. Rodrigo, Ateneo de Manila University, data coding methods
• Vincent Aleven, Carnegie Mellon University, taxonomy development

Abstract

We are investigating what factors lead students to make specific path choices in the learning space, focusing specifically on the shallow strategy known as gaming the system. Prior research has shown that a variety of motivations, attitudes, and affective states are associated with the choice to game the system (Baker et al, 2004; Baker, 2007; Rodrigo et al, 2007). However, other recent research has found that differences between lessons are on the whole better predictors of gaming than differences between students (Baker, 2007), suggesting that contextual factors associated with a specific tutor unit may be the most important reason why students game the system. Hence, this project is investigating how the content and presentational/interface aspects of a learning environment influence whether students tend to choose a gaming the system strategy.

To this end, we are in the process of annotating each learning event/transaction in a set of units in the Algebra LearnLab and the Middle School Cognitive Tutor with descriptions of its content and interface features, using a combination of human coding and machine learning. We are also in the process of adapting a detector of the shallow gaming strategy developed in a subset of the Middle School Cognitive Tutor to the LearnLabs, in order to use the gaming detector to predict exactly which learning events in the data involve shallow gaming strategies. After completing these steps, we will use data mining to connect gaming path choices with the content and interface features of the learning events they occur in. This will give us insight into why students make specific path choices in the learning space, and explain the prior finding that path choices differ considerably between tutor units.

Glossary

• Gaming the system
• Help abuse
• Systematic Guessing

Research Questions

What factors lead to the choice to game the system?

What factors make detectors of gaming behavior more or less likely to transfer successfully between tutor units?

Hypothesis

H1

Content or interface features better explain differences in gaming frequency than stable between-student differences

Background and Significance

In recent years, there has been considerable interest in how students choose to interact with learning environments. At any given learning event, a student may choose from a variety of learning-oriented "deep" paths, including attempting to construct knowledge to solve a problem on one’s own (Brown and vanLehn, 1980), self-explaining (Chi et al, 1989; Siegler, 2002), and seeking help and thinking about it carefully (Aleven et al, 2003). Alternatively, the student may choose from a variety of non-learning oriented "shallow" strategies, such as Help Abuse (Aleven & Koedinger, 2001), Systematic Guessing (Baker et al, 2004), and the failure to engage in Self-explanation.

One analytical tool with considerable power to help learning scientists explain the ways students choose to use a learning environment is the learning event space. In a learning event space, the different paths a student could take are enumerated, and the effects of each path are detailed, both in terms of how the path influences the student’s success within the environment, and the student’s learning. The learning event space model provides a simple way to identify the possible paths and effects; it also provides a concrete way to break down complex research questions into simpler and more concrete questions.

Gaming the system is an active and strategic type of shallow strategy known to occur in many types of learning environments (cf. Baker et al, 2004; Cheng and Vassileva, 2005; Rodrigo et al, 2007), including the Cognitive Tutors used in LearnLab courses (Baker et al, 2004). It was earlier hypothesized that gaming stemmed from stable differences in student goals, motivation, and attitudes -- however multiple studies have now suggested that these constructs play only a small role in predicting gaming behavior (Baker et al, 2005; Walonoski & Heffernan, 2006; Baker et al, 2008). By contrast, variation in short-term affective states and the tutor lesson itself appear to play a much larger role in the choice to game (Rodrigo et al, 2007; Baker, 2007).

In this project, we investigate what it is about some tutor lessons that encourages or discourages gaming. This project will help explain why students choose shallow gaming strategies at some learning events and not at others. This will contribute to our understanding of learning event spaces, and will make a significant contribution to the PSLC Theoretical Framework, by providing an account for why students choose the shallow learning strategies in many of the learning event space models in the PSLC Theoretical Framework. It will also jump-start the process of studying why students choose other shallow learning strategies beyond gaming the system, by providing a methodological template that can be directly applied in future research, as well as initial hypotheses to investigate.

Independent Variables

We have developed a taxonomy for how Cognitive Tutor lessons can differ from one another, the Cognitive Tutor Lesson Variation Space, version 1.0 (CTLVS1). The CTLVS1 was developed by a six member design team with a variety of perspectives and expertise, including three Cognitive Tutor designers (with expertise in cognitive psychology and artificial intelligence), a researcher specializing in the study of gaming the system, a mathematics teacher with several years of experience using Cognitive Tutors in class, and a designer of non-computerized curricula who had not previously used a Cognitive Tutor. Full detail on the CTLVS1's design is given in Baker et al (under review).

The CTLVS1's features are as follows:

Difficulty, Complexity of Material, and Time-Consumingness 1. Average percent error 2. Lesson consists solely of review of material encountered in previous lessons 3. Average probability that student will learn a skill at each opportunity to practice skill (cf. Corbett & Anderson, 1995) 4. Average initial probability that student will know a skill when starting tutor (cf. Corbett & Anderson, 1995) 5. Average number of extraneous “distractor” values per problem 6. Proportion of problems where extraneous “distractor” values are given 7. Maximum number of mathematical operators needed to give correct answer on any step in lesson 8. Maximum number of mathematical operators mentioned in hint on any step in lesson 9. Intermediate calculations must be done outside of software (mentally or on paper) for some problem steps (ever occurs) 10. Proportion of hints that discuss intermediate calculations that must be done outside of software (mentally or on paper) 11. Total number of skills in lesson 12. Average time per problem step 13. Proportion of problem statements that incorporate multiple representations (for example: diagram as well as text) 14. Proportion of problem statements that use same numeric value for two constructs 15. Average number of distinct/separable questions or problem-solving tasks per problem 16. Maximum number of distinct/separable questions or problem-solving tasks in any problem 17. Average number of numerical quantities manipulated per step 18. Average number of times each skill is repeated per problem 19. Number of problems in lesson 20. Average time spent in lesson 21. Average number of problem steps per problem 22. Minimum number of answers or interface actions required to complete problem Quality of Help Features 23. Average amount that reading on-demand hints improves performance on future opportunities to use skill (cf. Beck, 2006) 24. Average Flesch-Kincaid Grade Reading Level of hints 25. Proportion of hints using inductive support, going from example to abstract description of concept/principle (Koedinger & Anderson, 1998) 26. Proportion of hints that explicitly explain concepts or principles underlying current problem-solving step 27. Proportion of hints that explicitly refer to abstract principles 28. On average, how many hints must student request before concrete features of problems are discussed 29. Average number of hint messages per hint sequence that orient student to mathematical sub-goal 30. Proportion of hints that explicitly refer to scenario content (instead of referring solely to mathematical constructs) 31. Proportion of hint sequences that use terminology specific to this software 32. Proportion of hint messages which refer solely to interface features 33. Proportion of hint messages that cannot be understood by teacher 34. Proportion of hint messages with complex noun phrases 35. Proportion of skills where the only hint message explicitly tells student what to do Usability 36. First problem step in first problem of lesson is either clearly indicated, or follows established convention (such as top-left cell in worksheet) 37. Problem-solving task in lesson is not made immediately clear 38. After student completes step, system indicates where in interface next action should occur 39. Proportion of steps where it is necessary to request hint to figure out what to do next 40. Not immediately apparent what icons in toolbar mean 41. Screen is sufficiently cluttered with interface widgets, that it is difficult to determine where to enter answers 42. Proportion of steps where student must change a value in a cell that was previously treated as correct (examples: self-detection of errors; refinement of answers) 43. Format of answer changes between problem steps without clear indication 44. If student has skipped step, and asks for hint, hints refer to skipped step without explicitly highlighting in interface (ever seen) 45. If student has skipped step, and asks for hint, skipped step is explicitly highlighted in interface (ever seen) Relevance and Interestingness 46. Proportion of problem statements which involve concrete people/places/things, rather than just numerical quantities 47. Proportion of problem statements with story content 48. Proportion of problem statements which involve scenarios relevant to the "World of Work" 49. Proportion of problem statements which involve scenarios relevant to students’ current daily life 50. Proportion of problem statements which involve fantasy (example: being a rock star) 51. Proportion of problem statements which involve concrete details unfamiliar to population of students (example: dog-sleds) 52. Proportion of problems which use (or appear to use) genuine data 53. Proportion of problem statements with text not directly related to problem-solving task 54. Average number of person proper names in problem statements Aspects of “buggy” messages notifying student why action was incorrect 55. Proportion of buggy messages that indicate which concept student demonstrated misconception in 56. Proportion of buggy messages that indicate how student’s action was the result of a procedural error 57. Proportion of buggy messages that refer solely to interface action 58. Buggy messages are not immediately given; instead icon appears, which can be hovered over to receive bug message Design Choices Which Make It Easier to Game the System 59. Proportion of steps which are explicitly multiple-choice 60. Average number of choices in multiple-choice step 61. Proportion of hint sequences with final “bottom-out” hint that explicitly tells student what to enter in the software 62. Proportion of hint sequences with final hint that explicitly tells student what the answer is, but not what/how to enter it in the tutor software 63. Hint gives directional feedback (example: “try a larger number”) (ever seen) 64. Average number of feasible answers for each problem step Meta-Cognition and Complex Conceptual Thinking (or features that make them easy to avoid) 65. Student is prompted to give self-explanations 66. Hints give explicit metacognitive advice (ever seen) 67. Proportion of problem statements that use common word to indicate mathematical operation to use (example: “increase”) 68. Proportion of problem statements that indicate mathematical operation to use, but with uncommon terminology (example: “pounds below normal” to indicate subtraction) 69. Proportion of problem statements that explicitly tell student which mathematical operation to use (example: “add”) Software Bugs/Implementation Flaws (rare) 70. Percent of problems where grammatical error is found in problem statement 71. Reference in problem statement to interface component that does not exist (ever occurs) 72. Proportion of problem steps where hints are unavailable 73. Hint recommends student do something which is incorrect or non-optimal (ever occurs) 74. Student can advance to new problem despite still visible errors on intermediate problem-solving steps Miscellaneous 75. Hint requests that student perform some action 76. Value of answer is very large (over four significant digits) (ever seen) 77. Average length of text in multiple-choice popup widgets 78. Proportion of problem statements which include question or imperative 79. Student selects action from menu, tutor software performs action (as opposed to typing in answers, or direct manipulation)

We then labeled a large proportion of units in the Algebra LearnLab and the Middle School Cognitive Tutor with these taxonomic features. These features make up the independent variables in this project.

Dependent Variables

We have labeled approximately 1.2 million transactions in Algebra tutor data from the DataShop with predictions as to whether it is an instance of gaming the system. These predictions were created by using text replay observations (Baker, Corbett, & Wagner, 2006) to label a representative set of transactions, and then using these labels to create gaming detectors (cf. Baker, Corbett, & Koedinger, 2004; Baker et al, 2008) which can be used to label the remaining transactions.

Findings

Once all lessons are labeled according to the taxonomy features, and all transactions are labeled as gaming or not gaming, we will determine which features of a lesson predict whether students will game more or less. This will occur in Spring 2008.

A preliminary finding is that the difference between lessons is a significantly better predictor than the difference between students in determining how much gaming behavior a student will engage in, in a given lesson. Put more simply, knowing which lesson a student is using is a better predictor of how much gaming will occur, than knowing which student it is.

In the Middle School Tutor, lesson has 35 parameters and achieves an r-squared of 0.55. Student has 240 parameters and achieves an r-squared of 0.16. In the Algebra Tutor, lesson has 21 parameters and achieves an r-squared of 0.18. Student achieves an equal r-squared, but with 58 students; hence, lesson is a statistically better predictor because it achieves equal or significantly better fit with considerably fewer parameters.

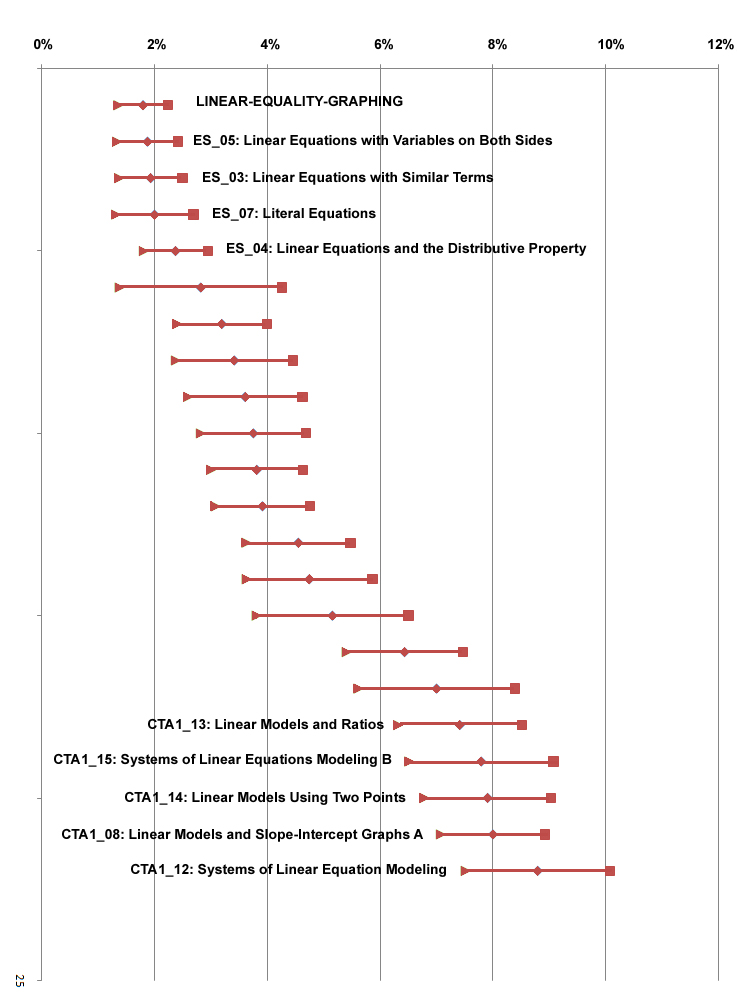This figure shows the prevalence of gaming across units in the Algebra LearnLab

Explanation

In the Algebra LearnLab, the degree of gaming does not seem to be obviously related to topic, or order in the curriculum, but appears to be linked to when the unit was developed -- each of the top five most gamed units comes from the original set of units developed for the Algebra I tutor.

A fuller explanation for this finding will be obtained when the project is completed.

References

Aleven, V., Koedinger, K.R. (2001) Investigations into Help Seeking and Learning with a Cognitive Tutor. In R. Luckin (Ed.), Papers of the AIED-2001 Workshop on Help Provision and Help Seeking in Interactive Learning Environments (2001) 47-58

Aleven, V., Stahl, E., Schworm, S., Fischer, F., Wallace, R. (2003) Help seeking and help design in interactive learning environments. Review of Educational Research, 73 (3), 277-320.

Baker, R.S.J.d. (2007) Is Gaming the System State-or-Trait? Educational Data Mining Through the Multi-Contextual Application of a Validated Behavioral Model. Complete On-Line Proceedings of the Workshop on Data Mining for User Modeling at the 11th International Conference on User Modeling 2007, 76-80. pdf

Baker, R.S.J.d., Corbett, A.T., Koedinger, K.R., Aleven, V., de Carvalho, A., Raspat, J. (under review) Educational Software Features that Encourage and Discourage "Gaming the System". Paper under review.

Baker, R.S., Corbett, A.T., Koedinger, K.R., Wagner, A.Z. (2004) Off-Task Behavior in the Cognitive Tutor Classroom: When Students “Game the System”. Proceedings of ACM CHI 2004: Computer-Human Interaction, 383-390.pdf

Baker, R.S.J.d., Corbett, A.T., Roll, I., Koedinger, K.R. (2008) Developing a Generalizable Detector of When Students Game the System. User Modeling and User-Adapted Interaction, 18, 3, 287-314. pdf

Baker, R.S., Corbett, A.T., Wagner, A.Z. (2006) Human Classification of Low-Fidelity Replays of Student Actions. Proceedings of the Educational Data Mining Workshop at the 8th International Conference on Intelligent Tutoring Systems, 29-36. pdf

Baker, R.S., Roll, I., Corbett, A.T., Koedinger, K.R. (2005) Do Performance Goals Lead Students to Game the System. Proceedings of the 12th International Conference on Artificial Intelligence in Education, 57-64. pdf

Baker, R.S.J.d., Walonoski, J.A., Heffernan, N.T., Roll, I., Corbett, A.T., Koedinger, K.R. (2008) Why Students Engage in "Gaming the System" Behavior in Interactive Learning Environments. To appear in Journal of Interactive Learning Research, 19 (2), 185-224. pdf

Beck, J.E. (2006) Using Learning Decomposition to Analyze Student Fluency Development. Workshop on Educational Data Mining at the 8th International Conference on Intelligent Tutoring Systems, 21-28.

Brown, J.S., vanLehn, K. (1980) Repair theory: A generative theory of bugs in procedural skills. Cognitive Science, 4, 379-426.

Cheng, R., Vassileva, J. (2005) Adaptive Reward Mechanism for Sustainable Online Learning Community. Proceedings of the 12th International Conference on Artificial Intelligence in Education, 152-159.

Chi, M.T.H., Bassok, M., Lewis, M.W., Reimann, P., Glaser, R. (1989) Self-Explanations: How Students Study and Use Examples in Learning to Solve Problems. Cognitive Science, 13, 145-182.

Corbett,A.T., & Anderson, J.R. (1995). Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction, 4, 253-278.

Koedinger, K. R., & Anderson, J. R. (1998). Illustrating principled design: The early evolution of a cognitive tutor for algebra symbolization. Interactive Learning Environments, 5, 161-180.

Rodrigo, M.M.T., Baker, R.S.J.d., Lagud, M.C.V., Lim, S.A.L., Macapanpan, A.F., Pascua, S.A.M.S., Santillano, J.Q., Sevilla, L.R.S., Sugay, J.O., Tep, S., Viehland, N.J.B. (2007) Affect and Usage Choices in Simulation Problem Solving Environments. Proceedings of Artificial Intelligence in Education 2007, 145-152. pdf

Siegler, R.S. (2002) Microgenetic Studies of Self-Explanations. In N. Granott & J. Parziale (Eds.), Microdevelopment: Transition processes in development and learning, 31-58. New York: Cambridge University.

Walonoski, J.A., Heffernan, N.T. (2006) Detection and Analysis of Off-Task Gaming Behavior in Intelligent Tutoring Systems. Proceedings of the 8th International Conference on Intelligent Tutoring Systems, 382-391.