Roll IPL

Invention as preparation for learning

Ido Roll, Vincent Aleven, Bruce M. McLaren, Kenneth Koedinger

Can invention activities prepare students to better learn from subsequent instruction, compared with instruction-and-practice only?

Meta-data

PI's: Ido Roll, Vincent Aleven, Dan Schwartz, Ken Koedinger

Other Contributers: David Klahr

Study #	Start Date	End Date	LearnLab Site	# of Students	Total Participant Hours	DataShop?
1	4/2007	4/2007	North Hills	20	40	No, paper-and-pencil only
2	9/2007	12/2007	Community Day	4	48	No, paper-and-pencil only
3	4/2008	5/2008	Steel Valley	125	900	No, paper-and-pencil only
4	4/2009	5/2009	Steel Valley	140	560	Some of it in DataShop, the rest is getting there

Abstract

The assistance dilemma asks what form of assistance is most appropriate for different stages of learning. While direct instruction and practice have been shown to be efficient for novices, students often acquire shallow knowledge components and lack robust understanding. Some evidence suggests that invention using contrasting cases, prior to instruction and practice, can accelerate future learning, compared with instruction and practice alone (Schwartz & Martin, 2004). The invention process as described in Schwartz & Martin (2004) includes the following stages: Design (of a mathematical model to solve a class of problems); calculation (of the solution based on the model); evaluation (of its correctness); and debugging (of the faulty model). Notably, most students fail to invent mathematically valid models, so the goal is not for students to discover the correct solution. At the same time, students do make models that capture deep features of the class of problems, which prepares them to learn and understand the significance of expert solutions for handling such situations. Following the invention, students receive instruction on the expert solution (that is, formulas) and practice it. This procedure is based on the hypothesis that students’ own inventions, together with subsequent instruction, are sources for coordinative learning. By attempting to create a model that correctly distinguishes the “contrasting cases” (carefully selected instances within a class of problems) students notice (and to some degree invent) the problem features that an adequate model must take into account, and they attend to them during subsequent instruction. However, alternative explanations for the effectiveness of the IPL process are possible, with different instructional implications. A “debugging hypothesis” suggests that evaluation and debugging of pre-designed models are sufficient to promote future learning by directing students’ attention to the short-comings of the designed models, and thus to the deep features of the domain. Alternatively, an “unfinished goals” hypothesis suggests that the effect is caused by students reaching impasses during invention. According to this hypothesis, calculation-evaluation are sufficient for preparing for future learning. We propose to investigate this in a series of ablation studies with the goal of better defining the invention process and identifying the cognitive processes involved. This includes a combination of in-vivo and lab studies within the Algebra LearnLab, contributing to the Coordinative Learning theoretical framework. Following the ablation studies we plan to implement the procedure in a Cognitive Tutor, which will be evaluated in a lab study. This will allow us to better operationalize the process, do a micro-genetic analysis of it, and identify productive patterns of learning trajectories using log mining.

Background and Significance

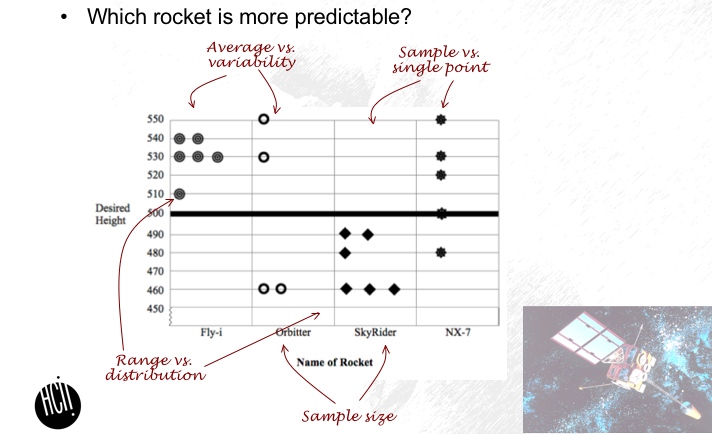
One of the main challenges of education is to help students reach meaningful and robust learning. The assistance dilemma raises the question of what form (and ‘amount’) of assistance are most effective with different learners in different stages of the learning process (Koedinger & Aleven, in press). Instruction followed by practice is known to be very efficient for teaching novices (e.g., Koedinger, Anderson, Hadley & Mark, 1997); yet, students often acquire shallow procedural skills, and fail to acquire conceptual understanding (Aleven & Koedinger, 2002). This can be attributed, at least in part, to students using superficial features and not encoding the deep features of the domain (Chi, Feltovich & Glaser, 1981). One approach to getting students to attend and encode the deep features is to add an invention phase prior to instruction. Invention as preparation for leaning (IPL) was shown to help students better cope with novel situations that require learning (Schwartz & Martin, 2004; Sears, 2006). In this process students are presented with a dilemma in the form of contrasting cases, and attempt to invent a mathematical model to resolve this dilemma. For example, Figure 1 shows four possible pitching machines. Students are asked to invent a method that will allow them to pick the most reliable machine. The concept of contrasting cases comes from the perceptual learning literature, since these cases, when appropriately designed, emphasize differences in the deep structure of the examples (Gibson & Gibson, 1955). The invention process includes designing a model, applying it to the given set of contrasting cases, evaluating the result, and debugging the model. This iterative process is very similar to the debugging process as described by Klahr and Carver (1988; Figure 2). Unlike other inquiry-based manipulations (cf. Lehrer et al., 2001; de Jong & van Joolingen, 1998), the goal of the IPL process is not for students to discover the correct model, but to prepare them for subsequent instruction. During the instruction students share their models, critic their peers’ models, and learn the expert solutions (A similar classroom critic process was shown to be effective by White & Frederiksen, 1998). Preparation for learning from the instruction is evaluated using accelerated future learning assessment. The accelerated future learning assessment includes an embedded instruction in the test in the form of solved example. Schwartz (2004) found that only students who invented prior to the test were able to take advantage of that instruction in order to solve novel problem, while students who practiced a given visual method prior to the test did not take advantage of the embedded learning resource and thus could not solve the target problem. This shows that the IPL process has a positive effect on students’ ability to independently learn from the solved examples. In the case of the contrasting cases given in Figure 1, subsequent instruction will introduce the students with the notion (and formulas) of variance. While the invention group was superior to instruction-and-practice group on accelerated future learning measure, there was no direct comparison of normal or transfer measures between invention and instruction-and-practice conditions (though invention students showed pre-to-post gains, and were shown to outperformed college students). Also, it is not yet clear how robust this pedagogy is and what its key features are.

Example for contrasting cases (topic - variability)

The overall IPL process:

Glossary

See IPL Glossary

Research questions

1. What is the overall effect of Invention tasks on students domain knowledge, sense-making skills, and motivation, compared with direct instruction?
2. What elements of invention contribute to that effect? What cognitive processes do they drive? In what ways does knowledge acquired following invention differ from knowledge acquired in direct instruction alone?
3. Can the IPL process be scaled-up using technology?

In addition, the project makes the following contributions:

1. It compares different measures of robust learning, in order to understand what aspect of knowledge can be assessed using what type of measure.

Independent Variables

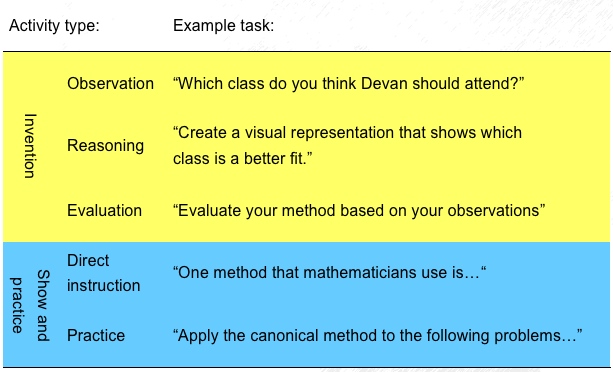
Different studies manipulated different stages of the Invention task: - Observation (a.k.a. comparative reasoning): comparing contrasting cases that vary along deep features, with regard to target concepts - Generative reasoning: designing novel mathematical procedures to compare the contrasting cases with regard to the target concept - Evaluation: Evaluation of the models

Dependent variables

Domain knowledge (in increasing 'distance' from instruction):

• Normal measures
• Transfer measures
• New strategy items (with learning resource)
• New strategy items (without learning resource)

Motivation and affect:

• Behavioral measure: % of students who kept working during breaks
• Self reports

Hypothesis

One hypothesis argues that generative reasoning (in the form of symbolic invention) is necessary to improve encoding of subsequent instruction. First, generative reasoning facilitates a process in which students express their prior ideas, identify their shortcomings, and refine their mental models, thus enabling conceptual change (Smith, diSessa, & Roschelle, 1994). For example, the self-explanation literature shows that asking students to explain their errors facilitates conceptual shift (c.f., Siegler, 2002). By attempting to invent and understand how different symbolic procedures succeed (or fail) to capture the differences between the contrasting cases, students also acquire a more cohesive and integrated understanding of the deep features of the domain. The importance of the symbolic nature of the process was demonstrated by Schwartz, Martin, and Pfaffman (2005), who asked students to reason verbally or mathematically about the balance beam problem. All students noticed the deep features of the balance beam domain - distance and weight. However, only students who reasoned mathematically were able to reconcile the two dimensions to a single representation. Interestingly, students’ thinking evolved even though their solutions were not complete, similar to the IPL effect. Lastly, the generative reasoning process may help students understand the function of the different components of the procedure (for example, dividing by N controls for sample size). Thus, students may encode the subsequent instruction by function and not merely by procedure. Functional mental models were previously shown to lead to better adaptation of knowledge (Kieras & Bovair, 1984). Hatano and Inagaki (1986) describe a similar process in which developing mental models of how procedures interact with empirical knowledge helps students acquire conceptual understanding of the domain. An alternative hypothesis argues that comparative reasoning is sufficient to achieve the learning benefits of IPL. According to this hypothesis, the benefits of invention stem from noticing and encoding the deep features of the domain. The comparative reasoning activity achieves that benefit by asking students to compare contrasting cases that differ with respect to their deep features. (Bransford & Schwartz, 2001). This qualitative analysis helps students set requirements for a valid model and thus acquire a better understanding (even if implicit) of the target concepts. Furthermore, according to this hypothesis, not only does the symbolic invention not contribute to future learning, it may waste students’ time (and thus reduce efficiency) or impose excessive cognitive load (Kirschner, Sweller & Clark, 2006). A second research question addressed by our current study examines the effect of IPL on the flexibility of students’ knowledge. We follow a distinction made by McDaniel and Schlager (1990) between transfer problems that require the application of a learned strategy (conventional transfer problems) and transfer problems that require the generation of a new strategy. McDaniel and Schlager found that while discovery tasks improve students’ performance on the latter, they have no effect on conventional transfer problems. Schwartz and Martin (2004) add a twist to these results. They found that IPL improves students’ ability to solve new-strategy problems as long as they are provided with instruction on how to do so. To further investigate the effect of IPL on knowledge flexibility, we evaluate students’ ability to independently solve new-strategy problems and encode new-strategy instructions. Our hypothesis, as supported by McDaniel and Schlager (1990), is that students who are engaged in IPL will acquire more flexible knowledge and thus will demonstrate better performance on new-strategy items. At the same time they will not show better ability to use existing strategies in novel contexts (conventional transfer items). Furthermore, following the findings of Schwartz and Martin (2004), we hypothesize that the effect of IPL will be mainly on encoding new-strategy instructions.

Instructional Principles

See IPL Instructional Principles

Findings

Domain knowledge:

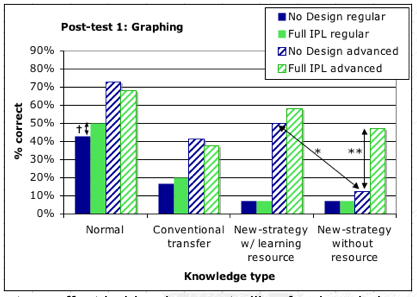
• IPL students in advanced classes were more capable of solving new strategy items without learning resource. In fact, in the absence of a learning resource, direct instruction students performed at floor, while IPL students performed as well as with the source.
• This effect holds when controlling for simple domain knowledge (performance on normal items in the same test).
• This was found in multiple new-strategy items. However, all results were found on a single topic (central tendency and graphing). The single test item on the topic of variability failed to capture difference between the groups.

Motivation:

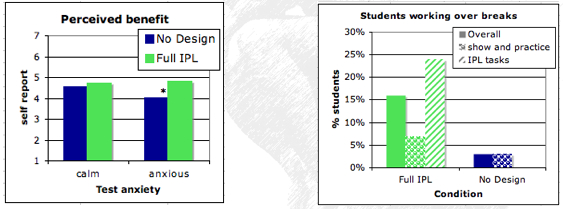
• IPL students reported to have benefited more (F=3.3, p<.07)
• There was a significant interaction between condition and test anxiety. Text anxiety was assessed using the MSLQ (Pintrich 1999) before the study began. Students who reported to have lower test anxiety also reported to have benefited more from IPL instruction compared to high-anxiety students in the no desin condition.
• IPL students stayed more often in class to work during breaks (IPL: 16% No Design: 3%).
• Furthermore, they did so during invention activities and not show-and-practice activities, suggesting that it is the activities that are motivating.

Explanation

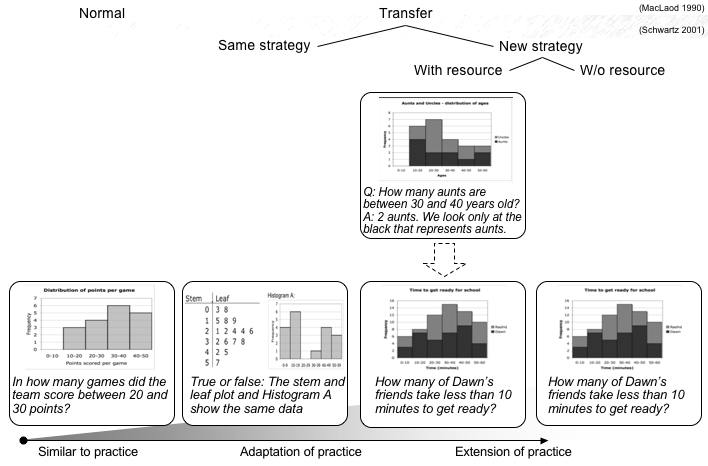
Regarding our first research question, we found that generative reasoning (on top of comparative reasoning) had a positive effect on students’ ability to solve new-strategy problems with no learning resource in the advanced classes. At the same time, as hypothesized, it had a marginal effect on normal or conventional transfer items. These results are interesting especially since Full IPL students had approximately half the time for instruction and practice compared with their No Design counterparts. Regarding the second research question, which dealt with students’ knowledge flexibility, we found that in the advanced classes, students who designed novel methods during IPL were more capable of solving problems that require the use of novel strategies. This finding echoes the effect found by McDaniel and Schlager (1990). Interestingly, the effect of IPL on new-strategy items with no resources holds even when controlling for performance on normal items on the same test. Thus, this effect can probably not be attributed to more domain knowledge. Instead, it is likely the outcome of a different encoding of domain knowledge, in a manner that is not reflected in normal or transfer items. On further scrutiny, students in both conditions did equally well on all tasks for which they received some form of instruction - whether in class (on normal and conventional transfer items) or embedded in the test (on new-strategy items with embedded learning resources). Regarding the latter, it seems that Full IPL students did not need the additional instruction whereas No Design students did not manage to solve the new-strategy problems without it. The performance of Full IPL students on new-strategy items remained virtually the same even in the absence of embedded instruction. This finding is at odds with earlier findings by Schwartz and Taylor (2004) who found that IPL improves students’ ability to encode future instruction but not solve novel problems without additional instruction. One explanation for the discrepancy between the studies is that the control group in Schwartz and Taylor (2004) did not engage in comparative reasoning. Therefore, it may be that the comparative reasoning stage helped students in our study to encode the novel instruction. An alternative explanation examines these results in terms of ‘distance’ from original classroom instruction. It may be that the embedded instruction on the first topic in our study was close to the classroom material, and thus simple enough for all students to encode. In contrast, the embedded learning resource in the study described by Schwartz and Martin (2004) was sufficiently far from the classroom instruction. Therefore, only IPL students, who had acquired more flexible knowledge, could learn from it and apply the acquired knowledge successfully. This explanation further suggests that in the absence of additional instruction, only Full IPL students in our study could make the leap and answer the target new-strategy items. While this argument explains performance on new-strategy items (with or without instruction) in terms of distance from classroom instruction, it does not explain what factors determine this distance. What makes some items ‘closer’ than others? What prepared Full IPL students for improved performance on some items but not on others? Students may grapple with many challenges during the invention phase, many of which do not receive attention during classroom instruction. Students who invent are exposed to various challenges by virtue of attempting to invent general valid methods. We hypothesize that students use knowledge acquired during these experiences when later integrating new-strategy tasks into their existing body of knowledge. For example, the post-tests in this study included three new-strategy items, requiring the following new strategies: (1) comparing multiple datasets in a single representation; (2) representing data in unconventional intervals; and (3) finding the ratio between variability and average in order to account for differences in magnitude. These topics were not covered during classroom instruction. However, when we analyzed students’ inventions, we noticed that many inventions included features that could prepare students to expand the instructed knowledge and invent the first two strategies (see Figure 3). Subsequently, Full IPL students demonstrated better performance on the relevant new-strategy items. At the same time, no student attempted during invention to compare datasets with different magnitudes. Correspondingly, Full IPL students did not exhibit better performance on this new-strategy item.

Connections

• Tim Nokes's study