Difference between revisions of "Analogical Scaffolding in Collaborative Learning"

From LearnLab
Jump to: navigation, search
m (→‎Connections)
 
(48 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
== Analogical Scaffolding in Collaborative Learning ==
 
== Analogical Scaffolding in Collaborative Learning ==
−
''Soniya Gadgil & Timothy Nokes''
+
''Soniya Gadgil & Timothy Nokes''
  
  
Line 25: Line 25:
 
<br>
 
<br>
 
=== Abstract ===
 
=== Abstract ===
−
Past research has shown that collaboration can enhance learning in certain conditions. However, not much work has explored the cognitive mechanisms that underlie such learning. Chi, Hausmann and Roy (2004) propose three mechanisms including: self-explaining, other-directed explaining, and co-construction. In the current study, we will examine the use of these mechanisms when participants learn from [[worked examples]] across different collaborative contexts. We compare the effects of adding prompts that encourage analogical comparison to prompts that focus on single examples (non-comparison) to a traditional instruction condition, as students learn to solve Physics problems in the domain of rotational kinematics. Students learning processes will be analyzed by examining their verbal protocols. Learning will be assessed via robust measures such as long-term retention and [[transfer]].  
+
Past research has shown that collaboration can enhance learning in certain conditions. However, not much work has explored the cognitive mechanisms that underlie such learning. Chi, Hausmann and Roy (2004) propose three mechanisms including: self-explaining, other-directed explaining, and co-construction. In the current study, we will examine the use of these mechanisms when participants learn from [[worked examples]] across different collaborative contexts. We compare the effects of adding prompts that encourage [[analogical comparison]] to prompts that focus on single examples (non-comparison) to a traditional instruction condition, as students learn to solve Physics problems in the domain of rotational kinematics. Students learning processes will be analyzed by examining their verbal protocols. Learning will be assessed via [[robust learning|robust]] measures such as long-term retention and [[transfer]].
  
 
=== Background and Significance ===
 
=== Background and Significance ===
 
Collaborative learning
 
Collaborative learning
−
Much research on collaborative learning has been conducted over the past few decades. The idea that putting two heads together could be better than one seems intuitive, and research has shown that when students learn in groups of two or more, they show better learning gains (at the group level) than working alone. Much of the past research has focused on identifying conditions that underlie successful collaboration. For example, we know that presence of cognitive conflict is an important variable underlying collaboration. Schwartz, Neuman, and Biezuner (2000) showed that when students with misconceptions distinct from each others’ collaborated, they were more likely to learn compared to those with the same misconception, or without a misconception. Studies have also found that establishing common ground is an important factor in learning from collaboration (Clark, 2000).
+
Past research on collaborative learning provides compelling evidence that when students learn in groups of two or more, they show better learning gains at the group level than when working alone. Much of this research has focused on identifying conditions that underlie successful collaboration. For example, we know that factors such as presence of cognitive conflict (Schwartz, Neuman, & Biezuner, 2000), establishing of common ground (Clark, 2000) and scaffolding (or structuring) of the interaction are important factors affecting collaborative learning. Providing scripted problem solving activities (e.g., one participant plays the role of the tutor vs. tutee and then switch) have also been shown to facilitate collaborative learning compared to unscripted conditions (McLaren, Walker, Koedinger, Rummel, Spada, & Kalchman, 2007). These results are typically explained in terms of the sense making processes in which the structured collaborative environments provide the learner more opportunities to construct the relevant knowledge components.
−
We also know that that scaffolding (or structuring) collaborative interaction is often critical for achieving effective learning gains (Palincsar & Brown, 1984; Hausmann, 2006; see Lin, 2001 for a review). For example, Hausmann (2006) conducted an experiment in which students solved a design problem in one of the three conditions: individually, in collaboration with a peer, and in collaboration with a peer but with specific instructions on conducting elaborative dialogues. Students in the elaborative dialogues condition outperformed the individuals and dyads who received no scaffolding. This is consistent with other results that show that providing scripted problem solving activities (e.g., one participant plays the role of the tutor vs. tutee and then switch) facilitate collaborative learning compared to an individual or unscripted conditions (McLaren, Walker, Koedinger, Rummel, Spada, & Kalchman, 2007).  
+
Although much work has focused on improving learning through collaboration, little research has examined the cognitive processes underlying successful collaboration. Most of the prior work has focused on the outcome or product of the group and less has been concerned with the underlying processes that give rise to the product. If we can uncover the cognitive processes underlying collaborative learning, it can further our understanding of how to improve collaborative learning environments.  
−
These results are typically explained in terms of the sense-making processes in which the structured collaborative environments provide the learner more opportunities to construct the relevant knowledge components.  
 
  
−
Learning Mechanisms Underlying Collaboration
+
'''Schema Acquisition and Analogical Comparison''': A problem schema is a knowledge organization of the information associated with a particular problem category. Problem schemas typically include declarative knowledge of principles, concepts, and formulae, as well as the procedural knowledge for how to apply that knowledge to solve a problem. One way in which schemas can be acquired is through analogical comparison (Gick & Holyoak, 1983). Analogical comparison operates through aligning and mapping two example problem representations to one another and then extracting their commonalities (Gentner, 1983; Gick & Holyoak, 1983; Hummel & Holyoak, 2003). Research on analogy and schema learning has shown that the acquisition of schematic knowledge promotes flexible transfer to novel problems. For example, Gick and Holyoak (1983) found that transfer of a solution procedure was greater when participants’ schemas contained more relevant structural features. Analogical comparison has also been shown to improve learning even when both examples are not initially well understood (Kurtz, Miao, & Gentner, 2001; Gentner Lowenstein, & Thompson, 2003). By comparing the commonalities between two examples, students could focus on the causal structure and improve their learning about the concept. Kurtz et al. (2001) showed that students who were learning about the concept of heat transfer learned more when comparing examples than when studying each example separately.
−
Although much work has focused on improving learning through collaboration, little research has examined the cognitive processes underlying successful collaboration. Most of the prior has focused on the outcome or product of the group and less has been concerned with the underlying processes that give rise to the product. If we can uncover the cognitive processes underlying collaborative learning, it can further our understanding of how to improve collaborative learning environments.  
+
In an ongoing project in the Physics LearnLab by Nokes & VanLehn, (2008) students learned to solve problems on rotational kinematics in one of the three conditions: read worked examples, self-explain worked examples, and engage in analogical comparison of worked examples. Preliminary results showed that the groups that self-explained and engaged in analogical comparison outperformed the read-only control on the far transfer tests. Our current project builds upon these results by applying them in a collaborative setting. In summary, prior work has shown that analogical comparison can facilitate schema abstraction and transfer of that knowledge to new problems. However, this work has not examined whether analogical scaffolding can lead to effective collaboration. The current work examines how analogical comparison may help students collaborate effectively.
−
Hausmann, Chi, and Roy (2004) have identified three mechanisms in which collaboration can work. The first is “other directed explaining” and occurs when one partner explains to the other how to solve a problem. The second is explanation through “co-construction” in which both partners equally share the responsibility of sense-making. Collaborators extend each others’ ideas and jointly work towards a common goal. The third mechanism is “self-explanation” in which one partner is engaged in a knowledge-building activity for their own learning. Data from physics problem-solving by undergrads showed that all three mechanisms are at play in collaborative problem-solving. However, the former two are more beneficial to both partners while the third is only beneficial to the partner doing the self-explaining.
 
−
In the current work we aim to build upon this research by examining dyads verbal protocols for how they engage in collaboration and the degree to which they use each of these mechanisms. In addition, we examine other cognitive factors that impact learning including error-correction (Ohlsson, 1996), constructing a joint mental model (Clark, 2000), and schema acquisition (Gick & Holyoak, 1983). In addition, the current work extends previous research by systematically investigating the degree to which analogical comparisons improve successful collaboration.  
 
  
−
Schema Acquisition and Analogical Comparison
+
=== Glossary ===
−
A problem schema is a knowledge organization of the information associated with a particular problem category. Problem schemas typically include declarative knowledge of principles, concepts, and formulae, as well as the procedural knowledge for how to apply that knowledge to solve a problem. Schemas have been hypothesized as the underlying knowledge organization of expert knowledge (Chase & Simon, 1973; Chi et al., 1981; Larkin et al., 1980). One way in which schemas can be acquired is through analogical comparison (Gick & Holyoak, 1983). Analogical comparison operates through aligning and mapping two example problem representations to one another and then extracting their commonalities (Gentner, 1983; Gick & Holyoak, 1983; Hummel & Holyoak, 2003). This process discards the elements of the knowledge representation that do not overlap between two examples but preserves the common elements. The resulting knowledge organization typically consists of fewer superficial similarities (than the examples) but retains the deep causal structure of the problems.
+
* [[collaboration]]
−
Research on analogy and schema learning has shown that the acquisition of schematic knowledge promotes flexible transfer to novel problems. Many researchers have found a positive relationship between the quality of the abstracted schema and transfer to a novel problem that is an instance of that schema (Catrambone & Holyoak, 1989; Gick & Holyoak, 1983; Novick & Holyoak, 1991). For example, Gick and Holyoak (1983) found that transfer of a solution procedure was greater when participants’ schemas contained more relevant structural features. Analogical comparison has also been shown to improve learning even when both examples are not initially well understood (Kurtz, Miao, & Gentner, 2001; Gentner Lowenstein, & Thompson, 2003). By comparing the commonalities between two examples, students could focus on the causal structure and improve their learning about the concept. Kurtz et al. (2001) showed that students who were learning about the concept of heat transfer learned more when comparing examples than when studying each example separately.
+
*[[analogical comparison]]
−
Several factors have been shown to improve schema acquisition including: increasing the number of examples (Gick & Holyoak, 1983), increasing the variability of the examples (Chen, 1999; Paas & Merrienboer, 1994), using instructions that focus the learner on structural commonalities (Cummins, 1992; Gentner et al., 2003), focusing the learner on the subgoals of the problems (Catrambone, 1996, 1998), and using examples that minimize students cognitive load (Ward & Sweller, 1990).
+
*[[in vivo experiment]]
−
An ongoing project by Nokes and VanLehn in the Physics LearnLab explores how students’ learning and understanding of conceptual relations between principles and examples can be facilitated (Nokes & VanLehn, 2008). Students in this research, learned to solve problems on rotational kinematics in one of the three conditions: read [[worked examples]], [[self-explain|self-explanations]] [[worked examples]], and engage in [[analogical comparison]] of [[worked examples]]. Preliminary results showed that the groups that self-explained and engaged in analogical comparison outperformed the read-only control on the far transfer tests. Our current project builds upon these results by applying them in a collaborative setting.
 
−
In summary, prior work has shown that analogical comparison can facilitate schema abstraction and transfer of that knowledge to new problems. However, this work has not examined whether analogical scaffolding can lead to effective collaboration. The current work examines how analogical comparison may help students collaborate effectively. We hypothesize that analogical prompts will facilitate not only analogical learning, but also other learning mechanisms such as explanation, co-construction, and error-correction.
 
  
 
=== Research Questions ===
 
=== Research Questions ===
Line 59: Line 54:
 
*Problem-Solving Condition: The problem-solving condition served as a control condition and collaborated to solve problems without any scaffolding. Students in This condition received the same worked examples as the two experimental groups, but without any prompts to guide them through the problem-solving process. They were given additional problems for practice, to equate the time on task with the other two conditions.
 
*Problem-Solving Condition: The problem-solving condition served as a control condition and collaborated to solve problems without any scaffolding. Students in This condition received the same worked examples as the two experimental groups, but without any prompts to guide them through the problem-solving process. They were given additional problems for practice, to equate the time on task with the other two conditions.
  
−
=== Hypothesis ===
+
=== Hypotheses ===
 
The following hypotheses are tested in the experiment:
 
The following hypotheses are tested in the experiment:
  
 
1. Analogical scaffolding will serve as a script to enhance learning via collaboration, therefore students in the compare condition will outperform students in the other two conditions. Students in the compare and non-compare conditions will both outperform students in the control condition.
 
1. Analogical scaffolding will serve as a script to enhance learning via collaboration, therefore students in the compare condition will outperform students in the other two conditions. Students in the compare and non-compare conditions will both outperform students in the control condition.
  
−
2. Students learning gains will differ by the kinds of learning processes they engaged in. Specifically, students engaging in self-explaining, other-directed explaining, and co-construction will show differential learning gains. This is an exploratory hypothesis and will be tested by undertaking a fine-grained analysis of verbal protocols generated by students as they solve problems collaboratively.  
+
2. Students learning gains will differ by the kinds of learning processes they engaged in. Specifically, students engaging in self-explaining, other-directed explaining, and co-construction will show differential learning gains. This is an exploratory hypothesis and will be tested by undertaking a fine-grained analysis of verbal protocols generated by students as they solve problems collaboratively.
  
 
===Dependent Variables===
 
===Dependent Variables===
−
* Normal post-test: Near transfer, immediate: After training, students were given a post-test that assessed their learning on various measures. Specifically, 5 kinds of questions were included in the post-test.  
+
* [[Normal post-test]]: Near transfer, immediate: After training, students were given a post-test that assessed their learning on various measures. Specifically, 5 kinds of questions were included in the post-test.  
−
* Robust learning
+
* [[Robust learning]]
 
**Long-term retention: On the student’s regular mid-term exam, one problem was similar to the training. Since this exam occurred a week after the training, and the training took place in just under 2 hours, the student’s performance on this problem is considered a test of long-term retention.
 
**Long-term retention: On the student’s regular mid-term exam, one problem was similar to the training. Since this exam occurred a week after the training, and the training took place in just under 2 hours, the student’s performance on this problem is considered a test of long-term retention.
 
**Near and far transfer: After training, students did their regular homework problems using Andes. Students did them whenever they wanted, but most completed them just before the exam.  
 
**Near and far transfer: After training, students did their regular homework problems using Andes. Students did them whenever they wanted, but most completed them just before the exam.  
−
**Accelerated future learning: The training was on electrical fields, and it was followed in the course by a unit on rotational dynamics. Log data from the rotational dynamics homework will be analyzed as a measure of acceleration of future learning.
+
**Accelerated future learning: The training was on rotational kinematics, and it was followed in the course by a unit on rotational dynamics. Log data from the rotational dynamics homework will be analyzed as a measure of acceleration of future learning.
 +
 
 +
===  Results ===
 +
 
 +
====Learning Results====
 +
[[Image:Example.jpg|left]]During learning, students in all three conditions studied worked examples and solved isomorphic problems. The answers to compare questions and sequential questions were scored for students in those conditions. Students were given one point for every correct concept they mentioned while answering the analogical comparison questions in the compare condition or questions directed at studying individual examples in the sequential condition.
 +
The sequential group answered a significantly higher percentage of questions (M = 70.28%, SE = 5%) correctly over the compare group (M = 50.66%, SE = 6%); F (1,22)= 5.60, p < 0.05. 
 +
Next, we looked at the isomorphic problems students solved during learning. On the first isomorphic problem, the three conditions were not significantly different; F (2,33) = 0.88, ns. On the second isomorphic problem, the three conditions were marginally different; F (2,33) = 2.60, p < 0.1 and the effect was in a direction favoring the sequential group over the compare and the problem solving groups.
 +
High variation was observed in performance on the learning tasks, suggesting the possibility that individual differences would interact with learning outcomes. We are interested in testing the effectiveness of our intervention on test performance for when testing was successful. Therefore, we selected the best learners from each group by conducting a median split based on the learning scores (i.e., average scores on isomorphic problems from the learning phase). This was based on the assumption that there are some qualitative differences between learners who show high learning and those who show low learning during the learning intervention. This left us with six pairs in each group (high / low split for each condition).
 +
 
 +
====Test Results ====
 +
The test phase was administered individually; therefore all scores reported below are means of scores for individual students.The test phase was divided into three sections: multiple-choice, problem solving, and open-ended questions.
 +
 
 +
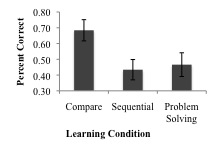
* Multiple-Choice Test. Overall, all three conditions performed poorly on the multiple-choice questions. The overall mean was 3.82 (SE = 0.23) out of a total of ten points. There were no significant difference between conditions, F (2,69) = 0.05, ns. Therefore, we shall focus only on the performance of High learners. Item analysis of the multiple choice questions shows that the high learners in the compare condition performed significantly better than the high learners in the sequential and problem solving conditions on five questions. An ANOVA showed a significant difference between the three conditions, in a direction favoring the compare condition, F (2,33) = 3.86, p < 0.05  (See Fig. 1 for means and standard errors). Consistent with our predictions this result shows more conceptual learning for the compare condition than the sequential and problem solving conditions. Contrasts revealed that the compare group was significantly different from the sequential group t (1,33) = 2.56, p < 0.05 and problem-solving group; t (1,33) = 2.22, p < 0.05 but the sequential and problem-solving groups were not significantly different; t (1,33) = -0.34, ns.
 +
 
 +
* Problem Solving Test. The problem-solving test consisted of two questions, one of which was isomorphic to one of the problems the students had encountered in the learning intervention, but had different surface features. The other problem had extraneous values, which required students to determine which of the values were critical to solving the problem before they plugged in the numbers.  We conducted a mixed model repeated measures ANOVA with problem-type as the within subject factor, and condition as the between-subject factor. There was a significant interaction problem-type X condition interaction (F (2,33)=3.37, p < 0.05). (See Fig. 2) Specifically, the students in the compare condition and sequential conditions performed better on the extraneous information problems than on the isomorphic problems, whereas students in the problem solving condition performed better on the isomorphic problem than they did on the extraneous information problem.
 +
* Open-Ended Questions Test. The first question in this test consisted of two problems for which students had to determine whether the answer was correct or wrong and provide an explanation for the same. The second question consisted of two problems for which students had to calculate an answer and provide an explanation. Chi square tests revealed no difference between conditions on either question. All χ2s (2, N = 36) <4.8, ns.
 +
 
 +
 
  
 
===Further Information===
 
===Further Information===
 +
==== Annotated Bibliography ====
 +
* Accepted as a poster presentation to CogSci 2009, Amsterdam.
 +
* Presentation to the PSLC Industrial Affiliates, February, 2009
 +
* Presentation to the PSLC Advisory Board, January, 2009
 +
* Poster to be presented at the Second Annual Inter-Science of Learning Center Student and Post-Doc Conference (iSLC, '09) at Seattle, WA, February 2009
 +
 
==== References ====
 
==== References ====
−
*Azmitia, M. (1988). Peer Interaction and Problem Solving: When Are Two Heads Better Than One? Child Development, 59(1), 87-96.
 
−
*Barron, B. (2000). Achieving Coordination in Collaborative Problem-Solving Groups. Journal of the Learning Sciences 9(4), 403-436.
 
−
*Catrambone, R. (1996). Generalizing solution procedures learned from examples. Journal of Experimental Psychology: Learning, Memory, and Cognition, 22, 1020-1031.
 
−
*Catrambone, R. (1998). The subgoal learning model: Creating better examples so that students can solve novel problems. Journal of Experimental Psychology: General, 127, 355-376.
 
−
*Catrambone, R., & Holyoak, K. J. (1989). Overcoming contextual limitations on problem solving transfer. Journal of Experimental Psychology: Learning, Memory, and Cognition, 15, 1147-1156.
 
 
*Chase, W. G., & Simon, H. A. (1973).  Perception in chess. Cognitive Psychology, 4, 55-81.
 
*Chase, W. G., & Simon, H. A. (1973).  Perception in chess. Cognitive Psychology, 4, 55-81.
 
*Chen, Z. (1999). Schema induction in children’s analogical problem solving. Journal of Educational Psychology, 91, 703-715.
 
*Chen, Z. (1999). Schema induction in children’s analogical problem solving. Journal of Educational Psychology, 91, 703-715.
Line 90: Line 104:
 
*Gentner, D., Loewenstein, J., & Thompson, L. (2003). Learning and transfer: A general role for analogical encoding. Journal of Educational Psychology, 95, 393-408.
 
*Gentner, D., Loewenstein, J., & Thompson, L. (2003). Learning and transfer: A general role for analogical encoding. Journal of Educational Psychology, 95, 393-408.
 
*Gick, M. L., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive Psychology, 15, 1-38.
 
*Gick, M. L., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive Psychology, 15, 1-38.
−
*Hausmann, R. G. M., Chi, M. T. H. & Roy, M. (2004). Learning from collaborative problem solving: An analysis of three dialogue patterns. In the Twenty-sixth Cognitive Science Proceedings. 
+
* Hausmann, R. G. M., Chi, M. T. H. & Roy, M. (2004). Learning from collaborative problem solving: An analysis of three dialogue patterns. In the Twenty-sixth Cognitive Science Proceedings.
−
*Hausmann, R. G. M. (2006, July). Why do elaborative dialogs lead to effective problem solving and deep learning? Poster presented at the 28th Annual Meeting of the Cognitive Science Conference, Vancouver, Canada.  
 
 
*Hummel, J. E., & Holyoak, K. J. (2003). A symbolic-connectionist theory of relational inference and generalization. Psychological Review, 110, 220-264.
 
*Hummel, J. E., & Holyoak, K. J. (2003). A symbolic-connectionist theory of relational inference and generalization. Psychological Review, 110, 220-264.
 
*Kurtz, K. J., Miao, C. H., & Gentner, D. (2001). Learning by analogical bootstrapping. Journal of the Learning Sciences, 10, 417-446.
 
*Kurtz, K. J., Miao, C. H., & Gentner, D. (2001). Learning by analogical bootstrapping. Journal of the Learning Sciences, 10, 417-446.
Line 106: Line 119:
  
 
==== Connections ====
 
==== Connections ====
−
==== Future Plans ====
+
This project shares features with the following research projects:
 +
 
 +
* [[Bridging_Principles_and_Examples_through_Analogy_and_Explanation|Bridging Principles and Examples through Analogy and Explanation (Nokes & VanLehn)]]
 +
* [[Craig observing | Learning from Problem Solving while Observing Worked Examples (Craig Gadgil, & Chi)]]
 +
 
 +
==== Future plans ====
 +
Our future plans for January 2009 - August 2009:
 +
* Code collaborative transcripts for different learning processes
 +
* Conduct laboratory study

Latest revision as of 23:23, 2 July 2010

Analogical Scaffolding in Collaborative Learning

Soniya Gadgil & Timothy Nokes


Summary Table

PIs Soniya Gadgil (Pitt), Timothy Nokes (Pitt)
Other Contributers Robert Shelby (USNA)
Study Start Date Sept. 1, 2008
Study End Date Aug. 31, 2009
LearnLab Site United States Naval Academy (USNA)
LearnLab Course Physics
Number of Students N = 72
Total Participant Hours 144 hrs.
DataShop Anticipated


Abstract

Past research has shown that collaboration can enhance learning in certain conditions. However, not much work has explored the cognitive mechanisms that underlie such learning. Chi, Hausmann and Roy (2004) propose three mechanisms including: self-explaining, other-directed explaining, and co-construction. In the current study, we will examine the use of these mechanisms when participants learn from worked examples across different collaborative contexts. We compare the effects of adding prompts that encourage analogical comparison to prompts that focus on single examples (non-comparison) to a traditional instruction condition, as students learn to solve Physics problems in the domain of rotational kinematics. Students learning processes will be analyzed by examining their verbal protocols. Learning will be assessed via robust measures such as long-term retention and transfer.

Background and Significance

Collaborative learning Past research on collaborative learning provides compelling evidence that when students learn in groups of two or more, they show better learning gains at the group level than when working alone. Much of this research has focused on identifying conditions that underlie successful collaboration. For example, we know that factors such as presence of cognitive conflict (Schwartz, Neuman, & Biezuner, 2000), establishing of common ground (Clark, 2000) and scaffolding (or structuring) of the interaction are important factors affecting collaborative learning. Providing scripted problem solving activities (e.g., one participant plays the role of the tutor vs. tutee and then switch) have also been shown to facilitate collaborative learning compared to unscripted conditions (McLaren, Walker, Koedinger, Rummel, Spada, & Kalchman, 2007). These results are typically explained in terms of the sense making processes in which the structured collaborative environments provide the learner more opportunities to construct the relevant knowledge components. Although much work has focused on improving learning through collaboration, little research has examined the cognitive processes underlying successful collaboration. Most of the prior work has focused on the outcome or product of the group and less has been concerned with the underlying processes that give rise to the product. If we can uncover the cognitive processes underlying collaborative learning, it can further our understanding of how to improve collaborative learning environments.

Schema Acquisition and Analogical Comparison: A problem schema is a knowledge organization of the information associated with a particular problem category. Problem schemas typically include declarative knowledge of principles, concepts, and formulae, as well as the procedural knowledge for how to apply that knowledge to solve a problem. One way in which schemas can be acquired is through analogical comparison (Gick & Holyoak, 1983). Analogical comparison operates through aligning and mapping two example problem representations to one another and then extracting their commonalities (Gentner, 1983; Gick & Holyoak, 1983; Hummel & Holyoak, 2003). Research on analogy and schema learning has shown that the acquisition of schematic knowledge promotes flexible transfer to novel problems. For example, Gick and Holyoak (1983) found that transfer of a solution procedure was greater when participants’ schemas contained more relevant structural features. Analogical comparison has also been shown to improve learning even when both examples are not initially well understood (Kurtz, Miao, & Gentner, 2001; Gentner Lowenstein, & Thompson, 2003). By comparing the commonalities between two examples, students could focus on the causal structure and improve their learning about the concept. Kurtz et al. (2001) showed that students who were learning about the concept of heat transfer learned more when comparing examples than when studying each example separately. In an ongoing project in the Physics LearnLab by Nokes & VanLehn, (2008) students learned to solve problems on rotational kinematics in one of the three conditions: read worked examples, self-explain worked examples, and engage in analogical comparison of worked examples. Preliminary results showed that the groups that self-explained and engaged in analogical comparison outperformed the read-only control on the far transfer tests. Our current project builds upon these results by applying them in a collaborative setting. In summary, prior work has shown that analogical comparison can facilitate schema abstraction and transfer of that knowledge to new problems. However, this work has not examined whether analogical scaffolding can lead to effective collaboration. The current work examines how analogical comparison may help students collaborate effectively.

Glossary

Research Questions

  • How can analogical comparison help students collaborate effectively?
  • Can analogical comparison facilitate but also other learning mechanisms such as explanation, co-construction, and error-correction during collaboration?


Independent Variables

The only independent variable was Experimental Condition. There were three conditions: Compare, Non-compare, and Problem-solving.

  • Compare Condition: Participants in this condition first read through and explained two worked examples. The worked examples did not have explanations for the solution steps and students were encouraged to generate the explanations and justifications for each step of the problem. They then performed the analogical comparison task, in which they were told that their task was to explicitly compare each part of the solution procedure to one another noting the similarities and differences between the two (e.g., goals, concepts, and solution procedures). Prompts in the form of questions to guide them through this process were provided. After a fixed amount of time, they were given the model answers to the questions and asked to check them against their own answers.
  • Non-Compare Condition: Participants in this condition first read through a worked-out example. Similar to the non-compare condition, they were not given the explanations of the steps, and generated the explanations while working collaboratively. After reading through and explaining the first example they answered questions designed to act as prompts for the students to explain the worked example. These prompts were equivalent to the comparison prompts however they were only focused on a single problem (e.g., “what is the goal of this problem”). After a fixed amount of time, they were given the model answers to the questions and asked to check them against their own answers. They were then given a second worked example isomorphic to the first one. Again, students studied the example and generated explanations. They then answered questions based on the second worked example. After a fixed amount of time, they were provided answers to those questions.
  • Problem-Solving Condition: The problem-solving condition served as a control condition and collaborated to solve problems without any scaffolding. Students in This condition received the same worked examples as the two experimental groups, but without any prompts to guide them through the problem-solving process. They were given additional problems for practice, to equate the time on task with the other two conditions.

Hypotheses

The following hypotheses are tested in the experiment:

1. Analogical scaffolding will serve as a script to enhance learning via collaboration, therefore students in the compare condition will outperform students in the other two conditions. Students in the compare and non-compare conditions will both outperform students in the control condition.

2. Students learning gains will differ by the kinds of learning processes they engaged in. Specifically, students engaging in self-explaining, other-directed explaining, and co-construction will show differential learning gains. This is an exploratory hypothesis and will be tested by undertaking a fine-grained analysis of verbal protocols generated by students as they solve problems collaboratively.

Dependent Variables

  • Normal post-test: Near transfer, immediate: After training, students were given a post-test that assessed their learning on various measures. Specifically, 5 kinds of questions were included in the post-test.
  • Robust learning
    • Long-term retention: On the student’s regular mid-term exam, one problem was similar to the training. Since this exam occurred a week after the training, and the training took place in just under 2 hours, the student’s performance on this problem is considered a test of long-term retention.
    • Near and far transfer: After training, students did their regular homework problems using Andes. Students did them whenever they wanted, but most completed them just before the exam.
    • Accelerated future learning: The training was on rotational kinematics, and it was followed in the course by a unit on rotational dynamics. Log data from the rotational dynamics homework will be analyzed as a measure of acceleration of future learning.

Results

Learning Results

Example.jpg

During learning, students in all three conditions studied worked examples and solved isomorphic problems. The answers to compare questions and sequential questions were scored for students in those conditions. Students were given one point for every correct concept they mentioned while answering the analogical comparison questions in the compare condition or questions directed at studying individual examples in the sequential condition.

The sequential group answered a significantly higher percentage of questions (M = 70.28%, SE = 5%) correctly over the compare group (M = 50.66%, SE = 6%); F (1,22)= 5.60, p < 0.05. Next, we looked at the isomorphic problems students solved during learning. On the first isomorphic problem, the three conditions were not significantly different; F (2,33) = 0.88, ns. On the second isomorphic problem, the three conditions were marginally different; F (2,33) = 2.60, p < 0.1 and the effect was in a direction favoring the sequential group over the compare and the problem solving groups. High variation was observed in performance on the learning tasks, suggesting the possibility that individual differences would interact with learning outcomes. We are interested in testing the effectiveness of our intervention on test performance for when testing was successful. Therefore, we selected the best learners from each group by conducting a median split based on the learning scores (i.e., average scores on isomorphic problems from the learning phase). This was based on the assumption that there are some qualitative differences between learners who show high learning and those who show low learning during the learning intervention. This left us with six pairs in each group (high / low split for each condition).

Test Results

The test phase was administered individually; therefore all scores reported below are means of scores for individual students.The test phase was divided into three sections: multiple-choice, problem solving, and open-ended questions.

  • Multiple-Choice Test. Overall, all three conditions performed poorly on the multiple-choice questions. The overall mean was 3.82 (SE = 0.23) out of a total of ten points. There were no significant difference between conditions, F (2,69) = 0.05, ns. Therefore, we shall focus only on the performance of High learners. Item analysis of the multiple choice questions shows that the high learners in the compare condition performed significantly better than the high learners in the sequential and problem solving conditions on five questions. An ANOVA showed a significant difference between the three conditions, in a direction favoring the compare condition, F (2,33) = 3.86, p < 0.05 (See Fig. 1 for means and standard errors). Consistent with our predictions this result shows more conceptual learning for the compare condition than the sequential and problem solving conditions. Contrasts revealed that the compare group was significantly different from the sequential group t (1,33) = 2.56, p < 0.05 and problem-solving group; t (1,33) = 2.22, p < 0.05 but the sequential and problem-solving groups were not significantly different; t (1,33) = -0.34, ns.
  • Problem Solving Test. The problem-solving test consisted of two questions, one of which was isomorphic to one of the problems the students had encountered in the learning intervention, but had different surface features. The other problem had extraneous values, which required students to determine which of the values were critical to solving the problem before they plugged in the numbers. We conducted a mixed model repeated measures ANOVA with problem-type as the within subject factor, and condition as the between-subject factor. There was a significant interaction problem-type X condition interaction (F (2,33)=3.37, p < 0.05). (See Fig. 2) Specifically, the students in the compare condition and sequential conditions performed better on the extraneous information problems than on the isomorphic problems, whereas students in the problem solving condition performed better on the isomorphic problem than they did on the extraneous information problem.
  • Open-Ended Questions Test. The first question in this test consisted of two problems for which students had to determine whether the answer was correct or wrong and provide an explanation for the same. The second question consisted of two problems for which students had to calculate an answer and provide an explanation. Chi square tests revealed no difference between conditions on either question. All χ2s (2, N = 36) <4.8, ns.


Further Information

Annotated Bibliography

  • Accepted as a poster presentation to CogSci 2009, Amsterdam.
  • Presentation to the PSLC Industrial Affiliates, February, 2009
  • Presentation to the PSLC Advisory Board, January, 2009
  • Poster to be presented at the Second Annual Inter-Science of Learning Center Student and Post-Doc Conference (iSLC, '09) at Seattle, WA, February 2009

References

  • Chase, W. G., & Simon, H. A. (1973). Perception in chess. Cognitive Psychology, 4, 55-81.
  • Chen, Z. (1999). Schema induction in children’s analogical problem solving. Journal of Educational Psychology, 91, 703-715.
  • Chi, M. T. H., Feltovich, P. J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121-152.
  • Chi, M. T. H., Roy, M., Hausmann, R. G. M. (2008). Observing Tutorial Dialogues Collaboratively: Insights About Human Tutoring Effectiveness From Vicarious Learning. Cognitive Science, 32, 301-341.
  • Cooke, N., Salas, E., Cannon-Bowers, J.A., Stout, R. (2000). Measuring team knowledge. Human Factors 42, 151-173.
  • Cummins, D. D. (1992). Role of analogical reasoning in the induction of problem categories. Journal of Experimental Psychology: Learning, Memory, and Cognition, 18, 1103-1124.
  • Dunbar, K. (1999). The Scientist InVivo: How scientists think and reason in the laboratory. In Magnani, L., Nersessian, N., & Thagard, P. Model-based reasoning in scientific discovery. Plenum Press.
  • Dunbar, K. (2001). The analogical paradox: Why analogy is so easy in naturalistic settings, yet so difficult in the psychology laboratory. In D. Gentner, Holyoak, K.J., & Kokinov, B. Analogy: Perspectives from Cognitive Science. MIT press.
  • Gentner, D., Loewenstein, J., & Thompson, L. (2003). Learning and transfer: A general role for analogical encoding. Journal of Educational Psychology, 95, 393-408.
  • Gick, M. L., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive Psychology, 15, 1-38.
  • Hausmann, R. G. M., Chi, M. T. H. & Roy, M. (2004). Learning from collaborative problem solving: An analysis of three dialogue patterns. In the Twenty-sixth Cognitive Science Proceedings.
  • Hummel, J. E., & Holyoak, K. J. (2003). A symbolic-connectionist theory of relational inference and generalization. Psychological Review, 110, 220-264.
  • Kurtz, K. J., Miao, C. H., & Gentner, D. (2001). Learning by analogical bootstrapping. Journal of the Learning Sciences, 10, 417-446.
  • Larkin, J., McDermott, J., Simon, D. P., & Simon, H. A. (1980). Expert and novice performance in solving physics problems. Science, 208, 1335-1342.
  • Lin, X. (2001). Designing metacognitive activities. Educational Technology Research & Development, 49, 1042-1629.
  • McLaren, B., Walker, E., Koedinger, K., Rummel, N., & Spada, H. (2005). Improving algebra learning and collaboration through collaborative extensions to the algebra tutor. Conference on computer supported collaborative learning.
  • Nokes, T. J. & VanLehn, K. (2008). Bridging principles and examples through analogy and explanation. In the Proceedings of the 8th International Conference of the Learning Sciences. Mahwah, Erlbaum.
  • Novick, L. R., & Holyoak, K. J. (1991). Mathematical problem solving by analogy. Journal of Experimental Psychology: Learning, Memory, and Cognition, 3, 398-415.
  • Ohlsson, S. (1996). Learning from performance errors. Psychological Review, 103, 241-262.
  • Paas, F. G. W. C., & Van Merrienboer, J. J. G. (1994). Variability of worked examples and transfer of geometrical problem solving skills: A cognitive-load approach. Journal of Educational Psychology, 86, 122-133.
  • Palincsar, A. S., & Brown, A. L. (1984). Reciprocal Teaching of Comprehension-Fostering and Comprehension-Monitoring Activities. Cognition and Instruction, 1, 117-175.
  • Schwarz, B. B., Neuman, Y., & Biezuner, S. (2000). Two Wrongs May Make a Right ... If They Argue Together! Cognition & Instruction, 18, 461-494.
  • Ward, M., & Sweller, J. (1990). Structuring effective worked examples. Cognition and Instruction, 7, 1-39.

Connections

This project shares features with the following research projects:

Future plans

Our future plans for January 2009 - August 2009:

  • Code collaborative transcripts for different learning processes
  • Conduct laboratory study
Retrieved from "https://learnlab.org/wiki/index.php?title=Analogical_Scaffolding_in_Collaborative_Learning&oldid=10773"