Harnessing what you know
Contents
Harnessing what you know: The role of analogy in robust learning
Robert Hausmann and Timothy J. Nokes
Abstract Knowledge transfer is a core assumption built into the pedagogy of most educational programs from K-12 to college. It is assumed that the material learned in the fourth week of the course is retained and transfers to material taught in the eighth week of the course. This is particularly true for highly structured courses such as physics; however, the empirical literature on learning suggests that far transfer is much more difficult than traditional pedagogy assumes (for reviews, see Bransford, Brown, & Cocking, 2000; Bransford & Schwartz, 1999; Gick & Holyoak, 1983). The goal of the present paper is to reconcile these apparently incompatible beliefs. Toward that end, we will use a repository of data, taken from the Physics LearnLab, to argue that the level of granularity of the constituent knowledge components affects the detection of to transfer from one domain to another.
Introduction
In well-structured domains, such as math or science, teachers often presume that the contents of one unit will transfer to units taught later in the semester; however, the learning literature is replete with evidence suggesting that transfer, especially ‘’far transfer’’, is difficult to achieve (Detterman, 1993). Do teachers have unrealistic expectations of their students, or are scientists looking in the wrong places to find evidence of far transfer? The primary goal of the present paper is to seek a resolution to this potential contradiction. Toward that end, we will define ‘’learning’’ at multiple levels of granularity and show how different levels of knowledge disaggregation reveal different conclusions about the existence or non-existence of far transfer.
Knowledge decomposition and learning curves
Many domains, such as math, science, and computer programming, assume that knowledge can be decomposed into a partially ordered set of skills or ‘’knowledge components’’. This assumption has been formalized in computational models of human cognition, including ‘’production rules’’ in the ACT-R architecture (Anderson & Lebiere, 1998) and ‘’chunks’’ in the SOAR architecture (Newell, 1990).
Evidence for the psychological plausibility for knowledge components can be found in the shape of the curve when an individual’s performance, which is typically measured as an error rate or the elapsed time, plotted against the opportunities to apply that particular piece of knowledge. These graphs are often referred to as ‘’learning curves’’, and an idealized learning curve monotonically decreases over time. Classic examples of learning curves include memorizing non-sense syllables (Ebbinghaus, 1913), learning how to roll a cigar (Crossman, 1959), and transmitting Morse code (Bryan & Harter, 1897).
A more contemporary example of a learning curve can be found in the domain of electrodynamics (Hausmann & VanLehn, under review). Students enrolled in a second-semester physic course were asked to solve problems with the Andes Physics Tutor (VanLehn et al., 2005). During an ‘’in vivo’’ experiment (Hausmann & VanLehn, 2007), students were asked to solve four electrodynamics problems, which included calculating the magnitude of an electric force (‘’F’’) that a charged particle (q) experiences when it is located in a region with an electric field (‘’E’’). The relationship between these three quantities is summarized by the following equation: ‘’F = E ∙ q’’. Before students are allowed to write an equation in the Andes, however, they must first define all of their variables, which includes drawing an electric-field vector. The learning curve for the experiment can be found in Figure 1.
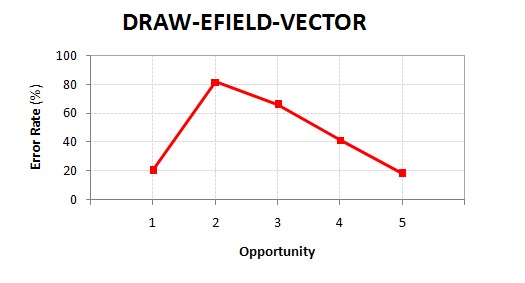
Upon first glance, three features are immediately evident in Figure 1. First, the first opportunity to draw an electric-field vector is actually the lowest error rate of all five opportunities. This directly contradicts the power law theory of learning. Second, there is a steady progression from a relatively high error rate for the second opportunity to the last. This segment of the graph is aligned with our expectations. Finally, the description of this dataset intimated that there were only four opportunities because the problem set given to the students during the experiment only consisted of four problems. This particular learning curve plots five opportunities. This final data-point represents only two students, so that suggests that these two individuals drew an extra electric-field vector while solving one of the four problems.
How do we reconcile this particular learning curve with the predictions of many learning theories? One potentially useful solution is to reanalyze the knowledge component itself. Vectors represent both magnitude and direction. The direction of a vector in Andes is set in a dialog box in the interface. For the first opportunity, the problem statement gives the precise angle in which the students are supposed to draw the vector. For all of the other opportunities, the students are responsible for calculating or inferring the direction of the electric-field vector. From a task analysis, we could argue that drawing an electric-field vector, when it is given in the problem statement, is a separate knowledge component from inferring the direction of a vector. The shape of the learning curve in Figure 2 supports this hypothesis.

The process or methodology used to reanalyze a knowledge component’s generality was based on (Corbett, McLaughlin, & Scarpinatto, 2000). When Corbert ‘’et al.’’ analyzed the learning curves of 34 students applying the quadratic formula, they found an inexplicable jump in the error rate at the fourth opportunity to apply the quadratic knowledge component (see Fig. 8 from Corbett et al., 2000, p. 101). To address this anomaly, they conducted a fine-grained analysis of the problems and discovered that on some of the problems, the constant term, ‘’c’’, was zero, and on other problems, the constant term was a positive integer. They inferred that the knowledge component APPLY-THE-QUADRATIC-FORMULA was an overly general rule and should be decomposed into two smaller skills. After making the decomposition, the error rate aligned with the theoretical prediction (see Fig. 9 from Corbett et al., 2000, p. 102).
Curriculum and knowledge-component mapping
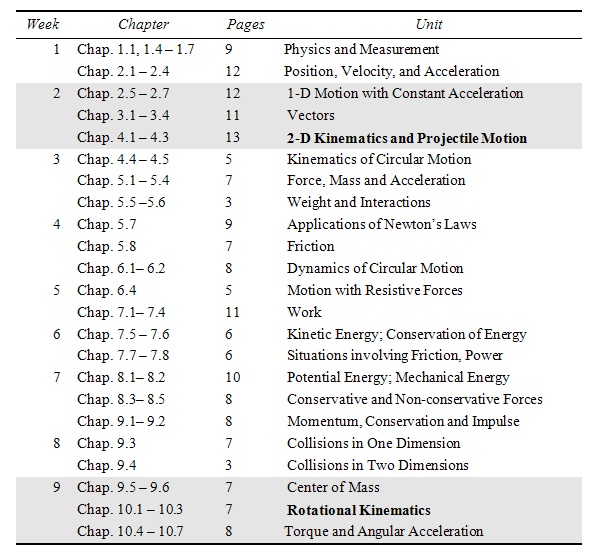
In a typical introductory physics course, translational kinematics (e.g., equations describing the motion of a particle along a straight trajectory) is taught during the second week of the semester. Rotational kinematics (e.g., equations describing the motion of an extended body in a circular trajectory) is typically taught during the eighth week of the course. For the present purposes, the data used for our analyses were taken from students enrolled in the first semester of introductory physics at the US Naval Academy. A condensed version of their syllabus is listed in Table 1.
The mapping between translational and rotational knowledge components is fairly straightforward for most knowledge components. There are, however, some interesting differences.
Linear (v) vs. Angular (ω) Velocity
The analogy between linear (i.e., translational) and angular (i.e., rotational) velocity is a straightforward mapping due to a special problem-solving heuristic. Angular velocity can be transformed into linear velocity by imagining the head of a screw that moves linearly as the rotating body turns. As the body turns, it unwinds the screw. The result is that the screw’s linear velocity is directly proportional to the angular velocity of the rotating body. If the conditions are set so that the threads on the screw are equal to one revolution of the body, then they can be placed in a 1:1 relationship. Given the translatability between the two, we predict positive transfer between linear and angular velocity.
Linear (a) vs. Angular (α) Acceleration
The heuristic for relating linear to angular velocity also works for acceleration. As the extended body speeds up or slows down, so does the head of the imaginary screw. Because of the tight connection between the two units, we predict there will be positive transfer for linear and angular acceleration.
Linear (s) vs. Angular (θ) Displacement
The same, however, is not true for linear and angular displacement. Instead of a one-to-one mapping between the two, a new concept needs to be learned. In the linear case of displacement (which first needs to be distinguished between ‘’distance’’ for many students), the displacement is a resultant vector that points from the beginning of the interval of interest to the end of the interval. The displacement of a particle can be imagined as a straight line, and it is measured in ‘’meters’’. Most students have a vast amount of experience by the time they take physics I. Angular displacement, on the other hand, is a measure of the angle through which an extended body turns over an interval of time, and it is measured in ‘’radians’’. Individuals typically do not have as much experience talking or thinking about movement as a change in angle. Therefore, we would not predict transfer in the case of displacement because angular displacement is a new idea that does not have as strong of a basis in everyday interactions with the physical world.
Analyses and Results
Data characteristics
The data analyzed for this project were taken from three semesters (Fall 2005 – 07) of college physics taught at the United States Naval Academy (USNA). Most students were sophomores, and they used the Andes Physics Tutor to solve their homework assignments. The data were downloaded from a central data repository called the DataShop, which is hosted by the Pittsburgh Science of Learning Center. For the analyses reported below (i.e., translational kinematics, translational dynamics, and rotational kinematics), the sample size consisted of two-hundred and twenty-one students (‘‘n‘‘ = 221) who generate 76,891 transactions.
Our analyses are structured as follows. First, we conducted an ANOVA for each knowledge component model, testing for differences between units. We also used opportunity as a within subject’s factor. To explore differences within each opportunity, we conducted pair-wise comparisons between units for each opportunity. Because of the large sample size, we adopted a conservative alpha level ( = .01). Finally, we restricted our analyses to the first three opportunities because the number of observations drops precipitously for each successive opportunity.
The instructional unit as the knowledge component
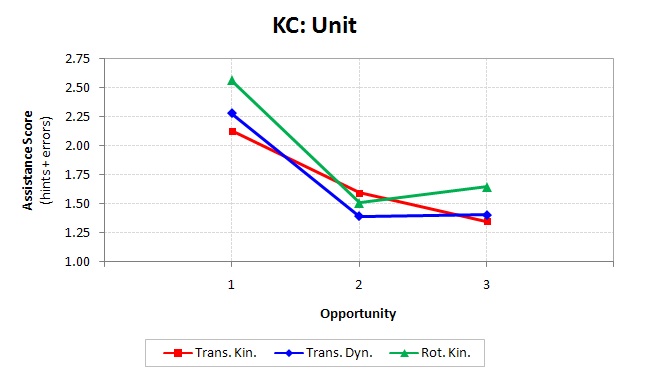
The first knowledge component treated each unit as a separate knowledge component. Because we were initially interested in far transfer, we included two units: translational and rotational kinematics. We also included a third unit, translational dynamics, as a control case. The reason for including translational dynamics is to control for XXX? Translational dynamics occurred after translational kinematics, but before rotational kinematics. Therefore, we would expect the learning curves for translational dynamics to fall somewhere between translational and rotational kinematics. The learning curves, over three opportunities, can be found in Figure 3.
For the first opportunity, there was a statistically reliable difference between the three units, ‘‘F‘‘(2, 1641) = 3.33, ‘‘p‘‘ < .001. Translational kinematics was the easiest of the three units because it had the lowest assistance score for the first opportunity. It demonstrated a reliably lower assistance score than rotational kinematics (‘‘p‘‘ = .01), but not rotational dynamics (‘‘p‘‘ = .35). There were no differences between the three units for the second and third opportunities.
The user-interface element as knowledge components
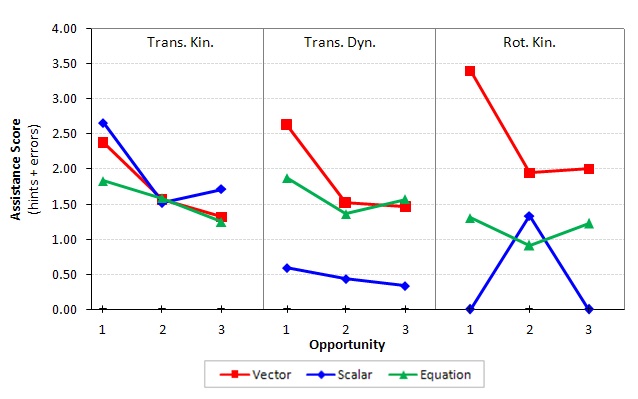
The overall shape of the learning curves for the three units were roughly monotonic, there was one problem. The theory of transfer would predict that rotational dynamics and rotational kinematics would demonstrate lower assistance scores because they came later in the semester. Therefore, we decided to break down these broad knowledge components into knowledge components related to the Andes user interface: drawing vectors, defining scalar quantities, and writing equations. The learning curves associated with these knowledge components can be found in Figure 4.
Overall, there was a reliable difference between units, opportunities, and knowledge components, ‘‘F‘‘(26, 4352) = 24.56, ‘‘p‘‘ < .001. The overall effect was qualified by a three-way interaction, ‘‘F‘‘(8, 4352) = 2.82, ‘‘p‘‘ = .004. Using Figure 4 as a guide, we restricted our analyses to just the vector knowledge components as the students progressed through the curriculum. It appears that the amount of assistance needed to correctly apply a vector knowledge component grew with time. For the first opportunity, more assistance was needed to draw vectors in rotational kinematics than in the case of translational kinematics (‘‘p‘‘ < .001) and dynamics (‘‘p‘‘ < .001). The shape of the curves for the other two knowledge components was reasonable for the first opportunity.
Physics concepts as knowledge components
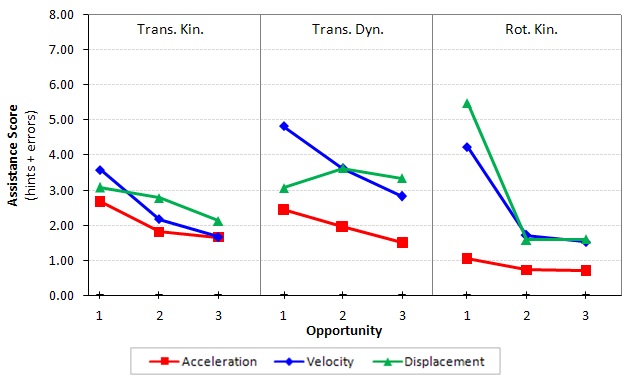
The analyses from the previous section suggest a closer examination of the vector learning curves. As the students move through the semester, they demonstrated slowly escalating assistance scores for drawing vectors. This is a very clear case where transfer is not occurring. Therefore, we decided to break down the vectors into their constituent physical concepts, which included drawing the acceleration, velocity, and displacement. The decomposed vector knowledge components are shown in Figure 5.
According to the learning curves, it appears there is no transfer between drawing a translational displacement vector and drawing an angular displacement vector. At least initially, there is a huge jump between the first opportunity to apply this particular knowledge component (DRAW-DISPLACEMENT & DRAW-ANG-DISPLACEMENT), and then the assistance score returns to a low, asymptotic level.
One potential explanation for the initial increase in assistance scores for displacement is in the way most rotational kinematics problems are worded. For example, the first problem in the USNA rotational homework set is, “A wheel is rotating counterclockwise at a constant rate of 3 rotations per second. Through what angle does the wheel rotate in 60.0 s?” It would be tempting for a novice to match the word “angle” in the problem statement, and use that as a basis for defining an angle in the Andes user interface. However, once the student attempts to define an angle, then the tutor will provide an unsolicited error message indicating that the angle is not part of the solution path for this problem. If the student then draws a displacement vector, then all of the errors and hints are blamed on the DRAW-ANG-DISPLACEMENT knowledge component (i.e., we use a temporal heuristic for the assignment of blame problem, Nwaigwe, Koedinger, VanLehn, Hausmann, & Weinstein, 2007).
Discussion
In the introduction, we pointed out the observation that there is an apparent contradiction between the empirical results investigating far transfer and the assumptions that teachers make within their own classroom. Teachers expect that their students should retain the knowledge components over several weeks, often with many other intervening units of instruction. However, the learning literature on far transfer seems to suggest that it is a rare occasion when knowledge lasts over long retention intervals.
To resolve the discrepancy between theory and practice, we introduced the hypothesis that the granularity of the assessed knowledge plays a large role in whether transfer is observed or not. For example, when the unit was taken as the knowledge component, then there was absolutely no evidence of transfer. The assistance scores associated with translational kinematics was initially lower (i.e., the first opportunity) than both the translational dynamics and rotational kinematics units. This initial advantage was maintained over fourteen of the sixteen opportunities.
Because there was no evidence of any sort of transfer, we decomposed the large, unit-size knowledge components into three smaller knowledge components that corresponded to the three broad categories of user-interface elements.
We repeated this process for the user interface elements that were vectors because the learning curves suggested that there was a drift toward increasing assistance score values. For the most part, the equations and scalar definitions were decreasing as the semester advanced. The vectors were disaggregated into acceleration, velocity, and displacement. These categories were more sensible because they finally corresponded to the concepts that are taught in the physics textbook.
Future work will include better understanding why the displacement vector showed such a steep learning curve. At first, students were asking for lots of help and committing many mistakes. However, after making those initial attempts, they seemed to learn how to apply this knowledge component fairly quickly. We also plan to extend our analyses to include the equations that were written. From the student’s perspective, writing equations is the most important part of the course.
References
- Anderson, J. R., & Lebiere, C. (1998). The atomic components of thought. Mahwah, N.J.: Lawrence Erlbaum Associates.
- Bryan, W. L., & Harter, N. (1897). Studies in the physiology and psychology of the telegraphic language. Psychological Review, 4(1), 27-53.
- Corbett, A. T., McLaughlin, M., & Scarpinatto, K. C. (2000). Modeling student knowledge: Cognitive tutors in high school and college. User Modeling and User-Adapted Interaction, 10, 81-108.
- Crossman, E. (1959). A theory of acquisition of speed-skill. Ergonomics, 2(2), 153-166.
- Detterman, D. K. (1993). The case for the prosecution: Transfer as an epiphenomenon. In D. K. Detterman & R. J. Sternberg (Eds.), Transfer on trial: Intelligence, cognition, and instruction (pp. 1-24). Norwood, NJ: Ablex.
- Ebbinghaus, H. (1913). Memory. A Contribution to Experimental Psychology. New York: Teachers College, Columbia University.
- Hausmann, R. G. M., & VanLehn, K. (2007). Explaining self-explaining: A contrast between content and generation. In R. Luckin, K. R. Koedinger & J. Greer (Eds.), Artificial intelligence in education: Building technology rich learning contexts that work (Vol. 158, pp. 417-424). Amsterdam: IOS Press.
- Hausmann, R. G. M., & VanLehn, K. (under review). The effect of generation on robust learning. International Journal of Artificial Intelligence and Education.
- Newell, A. (1990). Unified theories of cognition. Cambridge, MA: Harvard University Press.
- Nwaigwe, A., Koedinger, K. R., VanLehn, K., Hausmann, R. G. M., & Weinstein, A. (2007). Exploring alternative methods for error attribution in learning curves analysis in intelligent tutoring systems. In R. Luckin, K. R. Koedinger & J. Greer (Eds.), Artificial intelligence in education: Building technology rich learning contexts that work (pp. 246-253). Amsterdam: IOS Press.
- VanLehn, K., Lynch, C., Schultz, K., Shapiro, J. A., Shelby, R., Taylor, L., et al. (2005). The Andes physics tutoring system: Lessons learned. International Journal of Artificial Intelligence and Education, 15(3), 147-204.