Corrective self-explanation
Contents
Brief statement of principle
Explaining how and why incorrect solutions are incorrect will help students to reject incorrect knowledge components and, thus, stop using incorrect strategies to solve problems.
Description of principle
Operational definition
Corrective self-explanation is self-explanations of incorrect worked examples; explaining how and why they are incorrect. See the study by Booth.
Corrective self-explanation is a kind of error correction support which is a kind of instructional method.
Examples
Booth's Corrective self-explanation exercises: 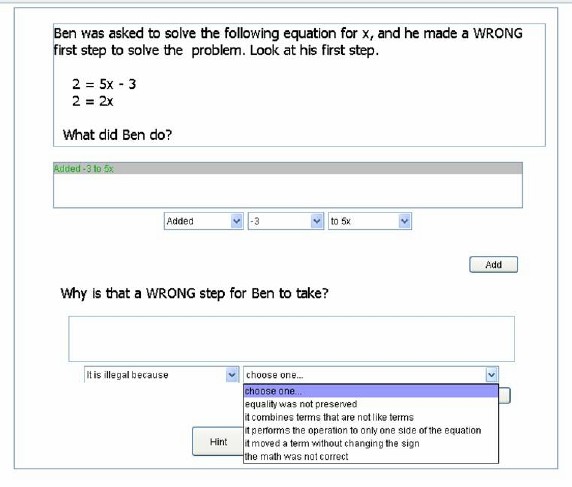
Experimental support
Laboratory experiment support
Siegler (2002) found that having students self-explain incorrect answers as well as correct answers increased learning of mathematical equality problems than explaining only correct answers.
Siegler & Chen (in press) also found that asking children to explain both why correct answers were correct and why incorrect answers were incorrect was more effective for learning to solve water displacement problems than only requesting explanations of correct answers.
In vivo experiment support
Preliminary results from Booth suggest that while completing any typical or corrective self-explanation exercises improve procedural performance for solving algebraic equations (Booth, Koedinger, & Siegler, 2007), corrective self-explanation may uniquely improve conceptual knowledge about features in the equations.
Theoretical rationale
(These entries should link to one or more learning processes.)
Conditions of application
Corrective self-explanation is likely only useful when students also recieve experience that will facilitate construction of correct knowledge components. If students recieve only corrective self-explanation, they may come to reject their incorrect knowledge components, but if they have nothing to replace them with, they will either flounder (having no way to solve the problem), or revert to use of the only strategy they know, even though they know it is incorrect.
Caveats, limitations, open issues, or dissenting views
Variations (descendants)
Generalizations (ascendants)
References
Booth, J.L., Koedinger, K., & Siegler, R.S. (2007, October). The effect of corrective and typical self-explanation on algebraic problem solving. Poster presented at the Science of Learning Centers Awardee’s Meeting in Washington, DC.
Siegler, R. S. (2002). Microgenetic studies of self-explanations. In N. Granott & J. Parziale (Eds.), Microdevelopment: Transition processes in development and learning (pp. 31-58). New York: Cambridge University.
Siegler, R.S., & Chen, Z. (in press). Developmental Science.