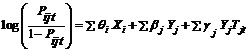Difference between revisions of "Using learning curves to optimize problem assignment"
(→Independent variables) |
(→Background and significance) |
||
| Line 21: | Line 21: | ||
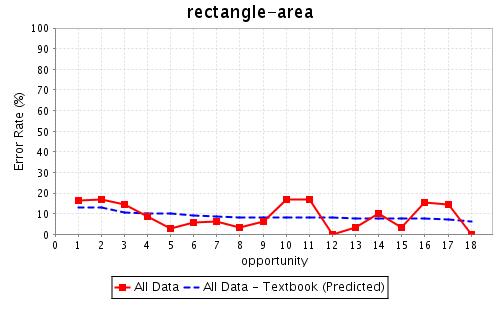
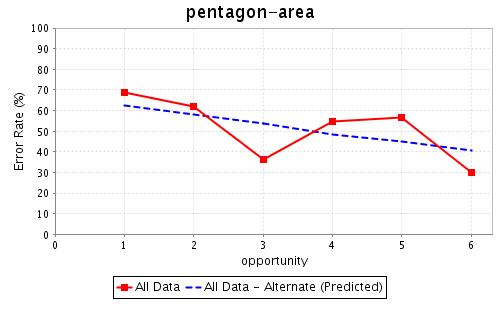
By applying LFA to the student log data from the Area unit of the 1997 Geometry Cognitive Tutor, we found two interesting phenomena. On the one hand, some easy (i.e. high βj) KCs with low learning rates (i.e. low γj) are practiced many times. Few improvements can be made in the later stages of those practices. KC rectangle-area is an example. This KC characterizes the skill of finding the area of a rectangle, given the base and height. As shown in Figure 1, students have an initial error rate around 12%. After 18 times of practice, the error rate reduces to only 8%. The average number of practices per student is 10. Many practices spent on an easy skill are not a good use of student time. Reducing the amount of practice for this skill may save student time without compromising their performance. Other over-practiced KCs include square-area, and parallelogram-area. On the other hand, some difficult (i.e. low βj) KCs with high learning rates (i.e. high γj) do not receive enough practice. Trapezoid-area is such an example in the unit. But students received up to a maximum of 6 practices. Its initial error rate is 76%. By the end of the 6th practice the error rate remains as high as 40%, far from the level of mastery. More practice on this KC is needed for students to reach mastery. Other under-practiced KCs include pentagon-area and triangle-area. | By applying LFA to the student log data from the Area unit of the 1997 Geometry Cognitive Tutor, we found two interesting phenomena. On the one hand, some easy (i.e. high βj) KCs with low learning rates (i.e. low γj) are practiced many times. Few improvements can be made in the later stages of those practices. KC rectangle-area is an example. This KC characterizes the skill of finding the area of a rectangle, given the base and height. As shown in Figure 1, students have an initial error rate around 12%. After 18 times of practice, the error rate reduces to only 8%. The average number of practices per student is 10. Many practices spent on an easy skill are not a good use of student time. Reducing the amount of practice for this skill may save student time without compromising their performance. Other over-practiced KCs include square-area, and parallelogram-area. On the other hand, some difficult (i.e. low βj) KCs with high learning rates (i.e. high γj) do not receive enough practice. Trapezoid-area is such an example in the unit. But students received up to a maximum of 6 practices. Its initial error rate is 76%. By the end of the 6th practice the error rate remains as high as 40%, far from the level of mastery. More practice on this KC is needed for students to reach mastery. Other under-practiced KCs include pentagon-area and triangle-area. | ||
| − | [[Image: Rectangle-area_learning_curve. | + | [[Image: Rectangle-area_learning_curve.jpg]] |
| − | [[Image: Pentagon-area_learning_curve. | + | [[Image: Pentagon-area_learning_curve.jpg]] |
Having students practice less than needed is clearly undesirable in the curriculum. Is over practice necessary? The old idiom “practice makes perfect” suggests that the more practice we do on a skill, the better we can apply the skill. Many teachers believe that giving students more practice problems is beneficial and “would like to have the students work on more practice problems”, even when “[students] were not making any mistakes and were progressing through the tutor quickly”[7]. | Having students practice less than needed is clearly undesirable in the curriculum. Is over practice necessary? The old idiom “practice makes perfect” suggests that the more practice we do on a skill, the better we can apply the skill. Many teachers believe that giving students more practice problems is beneficial and “would like to have the students work on more practice problems”, even when “[students] were not making any mistakes and were progressing through the tutor quickly”[7]. | ||
Revision as of 19:04, 13 February 2008
Contents
Abstract
This study examined the effectiveness of an educational data mining method – Learning Factors Analysis (LFA) – on improving the learning efficiency in the Cognitive Tutor curriculum. LFA uses a statistical model to predict how students perform in each practice of a knowledge component (KC), and identifies over-practiced or under-practiced KCs. By using the LFA findings on the Cognitive Tutor geometry curriculum, we optimized the curriculum with the goal of improving student learning efficiency. With a control group design, we analyzed the learning performance and the learning time of high school students participating in the Optimized Cognitive Tutor geometry curriculum. Results were compared to students participating in the traditional Cognitive Tutor geometry curriculum. Analyses indicated that students in the optimized condition saved a significant amount of time in the optimized curriculum units, compared with the time spent by the control group. There was no significant difference in the learning performance of the two groups in either an immediate post test or a two-week-later retention test. Findings support the use of this data mining technique to improve learning efficiency with other computer-tutor-based curricula.
Glossary
Data mining, intelligent tutoring systems, learning efficiency
Research question
How can we achieve a higher learning efficiency by reducing unnecessary over-practice in the intelligent tutoring settings?
Background and significance
Much intelligent tutoring system (ITS) research has been focused on designing new features to improve learning gains measured by the difference between pre and post test scores. However, learning time is another principal measure in the summative evaluation of an ITS. Intelligent tutors contribute more to education when they accelerate learning [9]. Bloom’s “Two Sigma” effect of a model human tutor [4] has been one of the ultimate goals for most intelligent tutors to achieve. So should be the “Accelerated Learning” effect shown by SHERLOCK’s offering four-year’s trouble shooting experience in the space of seven days of practice [12].
Cognitive Tutors are an ITS based on cognitive psychology results [11]. Students spend about 40% of their class time using the software. The software is built on cognitive models, which represent the knowledge a student might possess about a given subject. The software assesses students’ knowledge step by step and presents curricula tailored to individual skill levels [11]. According to Carnegie Learning Inc., by 2006, Cognitive Tutors have been widely used in over 1300 school districts in the U.S. by over 475,000 secondary school students. With such a large user base, the learning efficiency with the Tutor is of great importance. If every student saves four hours of learning over one year, nearly two million hours will be saved. To ensure adequate yearly progress, many schools are calling for an increase in instructional time. However, the reality is that students have a limited amount of total learning time, and teachers have limited amount of instructional time. Saving one hour of learning time can be better than increasing one hour of instructional time because it does not increase students’ or teachers’ work load. Moreover, if these saved hours are spent on learning other time-consuming subjects, they can improve the learning gains in those subjects.
Educational data mining is an emerging area, which provides many potential insights that may improve education theory and learning outcomes. Much educational data mining to date has stopped at the point of yielding new insights, but has not yet come full circle to show how such insights can yield a better intelligent tutoring system (ITS) that can improve student learning [2, 3]. Learning Factors Analysis (LFA) [6, 5] is a data-mining method for evaluating cognitive models and analyzing student-tutor log data. Combining a statistical model [10], human expertise and a combinatorial search, LFA is able to measure the difficulty and the learning rates of knowledge components (KC), predict student performance in each KC practice, identify over-practiced or under-practiced KCs, and discover “hidden” KCs interpretable to humans.
Pijt is the probability of getting a step in a tutoring question right by the ith student’s tth opportunity to practice the jth KC. The model says that the log odds of Pijt is proportional to the overall “smarts” of that student (θi) plus the “easiness” of that KC (βj) plus the amount gained (γj) for each practice opportunity. With this model, we can show the learning growth of students at any current or past moment.
By applying LFA to the student log data from the Area unit of the 1997 Geometry Cognitive Tutor, we found two interesting phenomena. On the one hand, some easy (i.e. high βj) KCs with low learning rates (i.e. low γj) are practiced many times. Few improvements can be made in the later stages of those practices. KC rectangle-area is an example. This KC characterizes the skill of finding the area of a rectangle, given the base and height. As shown in Figure 1, students have an initial error rate around 12%. After 18 times of practice, the error rate reduces to only 8%. The average number of practices per student is 10. Many practices spent on an easy skill are not a good use of student time. Reducing the amount of practice for this skill may save student time without compromising their performance. Other over-practiced KCs include square-area, and parallelogram-area. On the other hand, some difficult (i.e. low βj) KCs with high learning rates (i.e. high γj) do not receive enough practice. Trapezoid-area is such an example in the unit. But students received up to a maximum of 6 practices. Its initial error rate is 76%. By the end of the 6th practice the error rate remains as high as 40%, far from the level of mastery. More practice on this KC is needed for students to reach mastery. Other under-practiced KCs include pentagon-area and triangle-area.
Having students practice less than needed is clearly undesirable in the curriculum. Is over practice necessary? The old idiom “practice makes perfect” suggests that the more practice we do on a skill, the better we can apply the skill. Many teachers believe that giving students more practice problems is beneficial and “would like to have the students work on more practice problems”, even when “[students] were not making any mistakes and were progressing through the tutor quickly”[7]. We believe that if the teachers want more problems for their students to practice unmastered KCs or useful KCs not covered by the curriculum, more practice is necessary. To support KC long-term retention, more practice is necessary but needs to be spread on an optimal schedule [1, 14]. In the rectangle-area example, where all the practice for this KC is allocated in a short period, more practice becomes over practice, which is unnecessary after the KC is mastered.
Dependent variables
Normal post-test -- Shortly after finishing the 6th unit, the students took the post test.
Long-term retention -- In two weeks after each student finished the post test, we gave each student a retention test.
Independent variables
The independent variable was whether students used the version of the tutor with the optimized parameter settings or whether they used the version with the original parameter settings (an ecological control group).
Hypothesis
Over-practice is not necessary for short term retention as well as long term retention.
Reducing over-practice can improve learning efficiency.
Findings
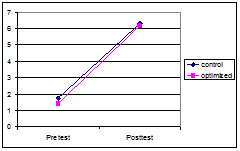
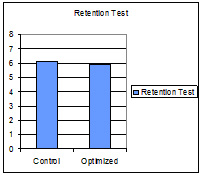
The optimized group learned as much as the control group but in less time. The two groups have similar scores in both the pre test and the post test. The amount of learning gain in both groups is approximately 5 points. To further examine the treatment effect, we ran an ANCOVA on the post test scores, with condition as a between subject factor, the pretest scores as a covariate, and an interaction term between the pretest scores and the condition. The post test scores are significantly higher than the pretest, p < .01, suggesting that the curriculum overall is effective. Meanwhile neither the condition nor the interaction are significant, p = 0.772, and p = 0.56 respectively. As shown in the Figure 2 (right), we found no significant difference in the retention test scores (p = 0.602, two tailed). The results from the post test and the retention tests suggest that there is no significant difference between the two groups on either of the two tests. Thus, over practice does not lead to a significantly higher learning gain.
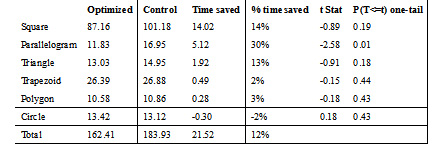
The actual learning time in each unit matches our hypotheses. As shown in Table 2, the students in the optimized condition spent less time than the students in the control condition in all the units except in the circle unit. The optimized group saved the most amount of time, 14 minutes, in unit 1 with marginal significance p = .19; 5 minutes in unit 2, p = .01, and 1.92, 0.49, 0.28 minutes in unit 3, 4, and 5 respectively. In unit 6, where we lowered P(L0), the optimized group spent 0.3 more minutes. Notice the percentage of the time saved in each unit. The students saved 30% of tutoring time in unit 2 Parallelogram, and 14% in unit 1 Square. In total students in the optimized condition saved around 22 minutes, an 12% reduction in the total tutoring time.
Explanation
Knowledge component hypothesis The over practice is the amount of practice done after students have mastered the skills under measurement. Once the skills reach the mastery level, any more practice on them may only leads to very little learning gain. Those gain are not even retained over the longer term. By removing those over practice, students can learn as much but save more time.
Descendants
Annotated bibliography
[1] J. R. Anderson, J. M. Fincham and S. A. Douglass, Practice and retention: A unifying analysis Journal of Experimental Psychology: Learning, Memory, and Cognition, 25 (1999), pp. 1120-1136.
[2] T. Barnes, The Q-matrix Method: Mining Student Response Data for Knowledge, American Association for Artificial Intelligence 2005 Educational Data Mining Workshop, 2005.
[3] J. E. Beck and B. P. Woolf, Evaluating tutorial actions with a user model, User Modeling and User Adapted Interaction, 2007.
[4] B. S. Bloom, The 2 Sigma Problem: The Search for Methods of Group Instruction as Effective as One-to-One Tutoring, Educational Researcher, 13 (1984), pp. 4-16
[5] H. Cen, K. Koedinger and B. Junker, Automating cognitive model improvement by a* search and logistic regression, American Association for Artificial Intelligence 2005 Workshop on Educational Datamining, 2005.
[6] H. Cen, K. Koedinger and B. Junker, Learning Factors Analysis - A General Method for Cognitive Model Evaluation and Improvement, 8th International Conference on Intelligent Tutoring Systems, 2006.
[7] J. Cital, A business email report to Carnegie Learning Inc, 2006, pp. Email.
[8] A. T. Corbett and J. R. Anderson, Knowledge tracing: Modeling the acquisition of procedural knowledge, User Modeling and User-Adapted Interaction, 1995, pp. 253-278.
[9] A. T. Corbett, K. Koedinger and J. R. Anderson, Intelligent Tutorins Systems, in M. G. Helander, T. K. Landauer and P. Prabhu, eds., Handbook of Human-Computer Interaction, Elsevier Science, Amsterdam, The Netherlands, 1997.
[10] K. Draney, P. Pirolli and M. Wilson, A Measurement Model for a Complex Cognitive Skill, Cognitively Diagnostic Assessment, Erlbaum, Hillsdale, NJ 1995.
[11] K. R. Koedinger and A. T. Corbett, Cognitive Tutors: Technology Bringing Learning Science to the Classroom, in K. Sawyer, ed., The Cambridge Handbook of the Learning Sciences, Cambridge University Press., 2006, pp. 61-78.
[12] A. Lesgold, S. Lajoie, M. Bunzo and G. Eggan, Sherlock: A Coached Practice Environment for an Electronics Troubleshooting Job, in J. H. Larkin and R. W. Chabay, eds., Computer-assisted instruction and intelligent tutoring systems: shared goals and complementary approaches, Lawrence Erlbaum Associates, 1988.
[13] A. Mitrovic, M. Mayo, P. Suraweera and B. Martin, Constraint-based tutors: a success story, 14th Int. Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems IEA/AIE-2001, Springer-Verlag Berlin Heidelberg, Budapest, 2001.
[14] P. I. Pavlik and J. R. Anderson, Practice and Forgetting Effects on Vocabulary Memory: An Activation Based Model of the Spacing Effect Cognitive Science, 29 (2005), pp. 559-586.
[15] A. Rafferty and M. Yudelson, Applying LFA for Building Stereotypical Student Models, PSLC Summer School 2006 Projects, Pittsbugh Science of Learning Center, Pittsburgh PA, 2006.